Funzione di densità
per variabili casuali continue (PDF)
Un vero viaggio non è cercare nuove terre, ma avere nuovi occhi. Blaise Pascal  (1623 - 1662)
Abbiamo visto nella pagina precedente :"Funzione di massa di probabilità", che per le variabili casuali continue non ha senso determinare la probabilità su ciascun valore assunto dalla variabile casuale semplice X (visto che è sempre nulla), ma è corretto parlare di probabilità che la variabile casuale assuma valori in un intervallo, anche piccolissimo, del tipo (x, x + dx]. O meglio, la cosa che importa di più è valutare quanto cambia la probabilità da un valore all'altro, cioè interessa il rapporto incrementale:
 P(x <  X ≤ x + dx) / dx.
Infatti, una variabile casuale continua X è una funzione che può assumere tutti i valori compresi in un intervallo (a,b). I casi possibili sono di fatto infiniti e quindi:
 


Esempio 1: La probabilità che la temperatura nella stanza sia esattamente 20 °C è nulla, invece sarà maggiore di zero la probabilità che la temperatura sia compresa fra 20°C e 20.1°C.

Data la variabile casuale continua X che assume valori nell'intervallo (a,b)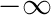   ≤ a < b ≤ 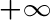, la funzione di densità di probabilità (o PDF) è la funzione  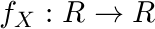che ad ogni reale associa il limite per dx che tende a 0, del rapporto tra la probabilità che la variabile casuale assuma valori nell'intervallo (x, x + dx] e l'ampiezza dx.
In simboli :

La funzione di densità in x, allora, rappresenta quanto vale la probabilità "intorno ad x" in rapporto all'ampiezza di tale "intorno". Il termine funzione di densità, serve proprio ad evocare quanto è densa la probabilità.
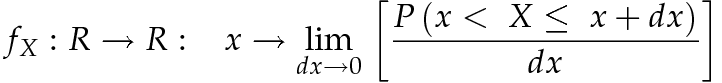
Ogni evento deve essere ricondotto all'unione, negazione o intersezione di intervalli del tipo (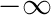 , x) . Abbiamo:


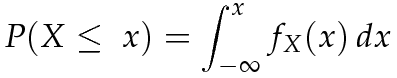
oppure:


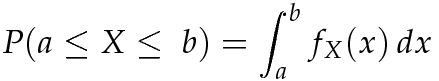
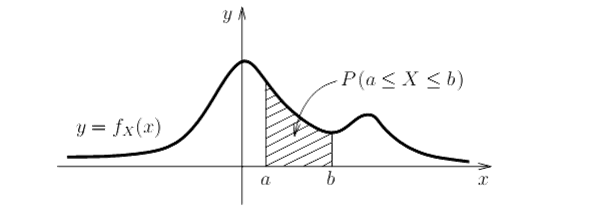
La probabilità che una variabile aleatoria continua X assume valori in un intervallo reale (a,b) è data dall'area sottesa al grafico della funzione di densità .


Osservazione:
La funzione di densità, non è una probabilità, è pero una funzione legata alla probabilità, perché se voglio calcolare la probabilità che la variabile casuale continua X appartenga ad un intervallo, basta che faccia l'integrale della funzione di densità. 

Proprietà della funzione di densità:

1. Una funzione di densità non può mai assumere valori negativi, ossia 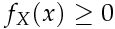ciò assicura che la probabilità X cada in un qualsiasi intervallo sia non-negativa.

2. L'area totale sottesa alla funzione è uguale a 1, ossia:
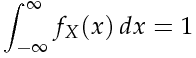
(in quanto quest'integrale rappresenta la probabilità dell'evento certo).
Il fatto che l'integrale della funzione di densità nell'intervallo
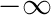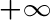(, ) vale 1 viene nominata condizione di normalizzazione. Per avere questo, ossia per avere la convergenza dell'integrale, la funzione che rappresenta una densità di probabilità deve tendere a zero quando la variabile indipendente tende a più o meno infinito.

3. La probabilità che la variabile casuale continua X assuma un particolare valore dell'intervallo è uguale a zero. Ciò è dovuto al fatto che un singolo valore corrisponde ad un intervallo di ampiezza zero, quindi la corrispondente area è anch'essa zero. Questo per esempio implica che non ha influenza l'inclusione, nel calcolo della probabilità, degli estremi dell'intervallo, ossia:

P(a ≤ X ≤ b) = P(a<X< b)=P(a ≤ X< b)=P(a < X ≤ b)


Osservazione:
La funzione di densità può essere costante o non costante.


Esempio 2: funzione di densità di probabilità costante:
Sia X una variabile casuale che può assumere tutti i valori dell'intervallo reale [0;20] in modo tale che tutti i sottointervalli di uguale ampiezza abbiano la stessa probabilità (diversa da zero). Se consideriamo la seguente funzione:
 
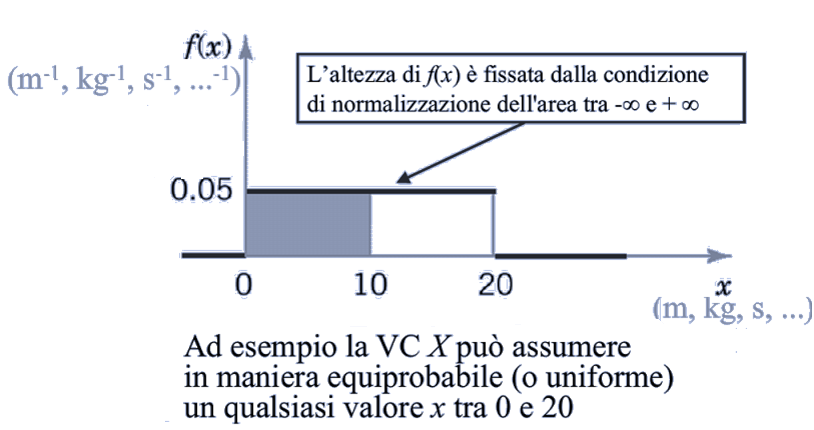
Dunque la funzione di densità della variabile casuale X, sarà:

Esempio 3:

Quando arriva la telefonata?
Il signor Rossi aspetta una telefonata dal signor Bianchi il quale ha preannunciato che chiamerà, in un istante non meglio precisato, fra le 16:00 e le 18:00. Il signor Rossi si deve però assentare dalle 16:45 alle ore 17:00. Qual'è la probabilità che la telefonata arrivi mentre il signor Rossi è assente ?
L'istante della telefonata è una variabile casuale X. Per quanto ne sa il signor Rossi, tutti i momenti dalle 16:00 alle 18:00 sono equiprobabili, mentre fuori da questo intervallo la probabilità è zero. Dunque è intuitivo considerare X come una variabile casuale continua, la cui densità   ha un valore costante : c sull'intervallo [16,18] ed ha il valore zero fuori di questo intervallo. Quanto vale la costante c ? Deve essere tale da soddisfare la relazione :
, ovvero l'area del rettangolo con base [16,18] e l'altezza c sia 1. Dunque 2c=1 e perciò abbiamo c= 1/2. La funzione di densità della variabile X, sarà:



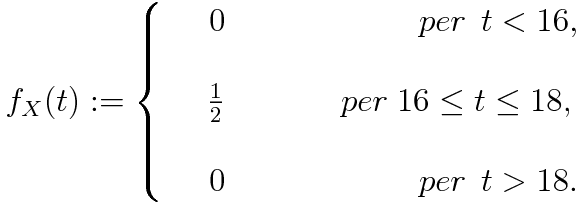
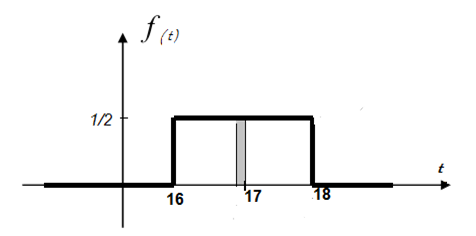
L'area grigia corrisponde alla probabilità P(16:45 ≤  X ≤ 17:00) e si nota che il valore di questa probabilità è 1/8 (l'area del rettangolo è 1)

Osservazione:
In genere abbiamo il grafico della funzione di densità costante :
Esempio 4: funzione di densità di probabilità non costante:
Consideriamo una variabile casuale X che può assumere tutti i valori dell'intervallo reale [0;1] con probabilità descritta dalla seguente funzione di densità:

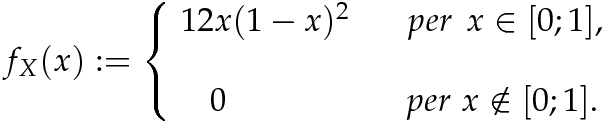
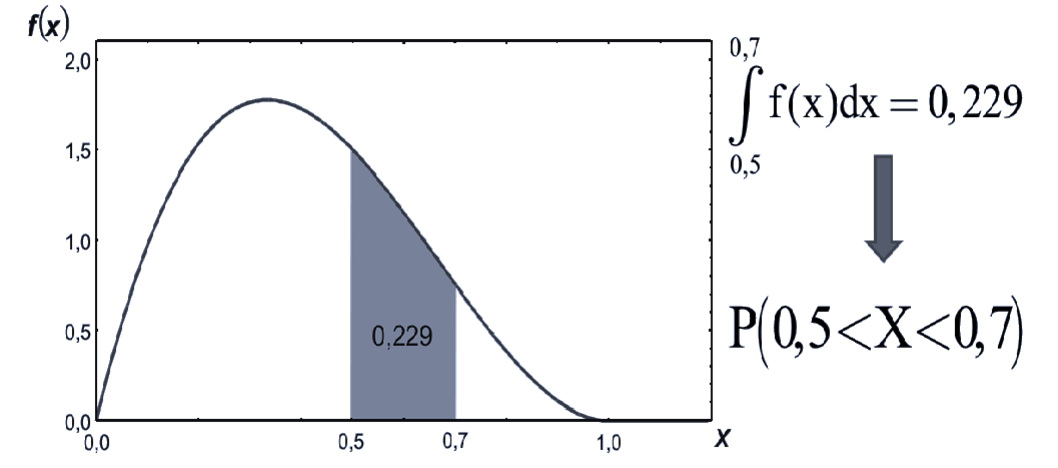
La variabile casuale X ha quindi una funzione di densità che non assegna una probabilità costante all'interno dell'intervallo [0;1] (a parità di ampiezza dei sottointervalli). Si può osservare dal grafico sottostante che la probabilità è più bassa in corrispondenza a sottointervalli vicini agli estremi. Come è mostrato nel seguente grafico, la probabilità che la variabile casuale X assuma un valore nell'intervallo [0,5;0,7] è pari a 0,229, che corrisponde all'area sottesa alla funzione in quell'intervallo.
 



    Una funzione di densità di probabilità continua è un modello che definisce analiticamente come si distribuiscono i valori assunti da una variabile aleatoria continua.
 Quando si dispone di un'espressione matematica adatta alla rappresentazione di un fenomeno continuo, siamo in grado di calcolare la probabilità che la variabile aleatoria assuma valori compresi in intervalli.
  I modelli continui hanno importanti applicazioni in ingegneria, fisica, economia e nelle scienze sociali.
    Alcuni tipici fenomeni continui sono l'altezza, il peso, le variazioni giornaliere nei prezzi di chiusura di un'azione, il tempo che intercorre fra gli arrivi di aerei presso un aeroporto, il tempo necessario per servire un cliente in un negozio, ecc.
    L'immagine sottostante rappresenta graficamente tre funzioni di densità di probabilità: normale, uniforme, ed esponenziale.




pagina precedente            Torna all'Indice         pagina successiva