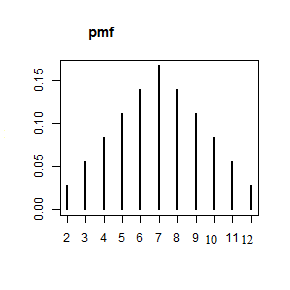- Funzione di massa (o di probabilità)
- per variabili casuali discrete (o PMF)
-
Dov’è la sapienza che abbiamo smarrita nella conoscenza?
Dov’è la conoscenza che abbiamo smarrita nell’informazione?
Dov’è l’informazione che abbiamo smarrito nei dati?”( Mark Porat, frase incisa nell’ala delle Comunicazioni nel Museo scientifico dei Bambini di Washington).
Il singolo esito di un processo aleatorio non è prevedibile a priori, anche dopo ripetute esecuzioni nelle stesse condizioni. Si possono comunque individuare delle "regolarità" nell'insieme dei risultati di un numero elevato di ripetizioni dello stesso esperimento, ovvero si può "modellare" la "casualità" presente in una misura sperimentale attraverso una funzione di probabilità che regola il processo aleatorio.
Sia X una variabile casuale discreta che assume i valori: x1, …, xk (eventualmente k è
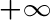 se la variabile casuale assume un’infinità numerabile di valori).
se la variabile casuale assume un’infinità numerabile di valori). La funzione di massa di X , è la funzione
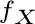 dall’insieme
dei reali nei reali positivi, che ad ogni elemento associa la
probabilità che la variabile casuale discreta assuma valori uguali al reale
dall’insieme
dei reali nei reali positivi, che ad ogni elemento associa la
probabilità che la variabile casuale discreta assuma valori uguali al reale 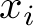 ; in simboli:
; in simboli: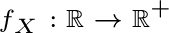
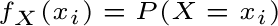
Tale funzione vale quindi:
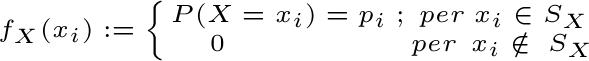
Gli elementi dell'insieme {x1, x2,…,xk,…} vengono indicati con il nome di punti di massa.
La funzione di massa di una variabile casuale discreta, quindi, è semplicemente P(X=x), cioè la probabilità che X sia uguale ad x: solo per brevità è indicata con f(x), ma dobbiamo sempre pensare che suo significato è, appunto, P(X=x). Come indicato nella definizione, tale probabilità sarà maggiore di 0 solo per i valori x che la variabile casuale può assumere, mentre sarà 0 per tutti gli altri valori di x.

La seconda proprietà significa che la funzione di massa soddisfa la condizione di normalizzazione, la somma essendo estesa a tutti i possibili valori assunti da X, questa condizione ci dice che la probabilità che X assuma almeno uno dei valori possibili è uguale ad 1.
Si può rappresentare la funzione di massa di una variabile casuale ponendo in ascissa i valori reali che assume, ed in ordinata le rispettive probabilità:
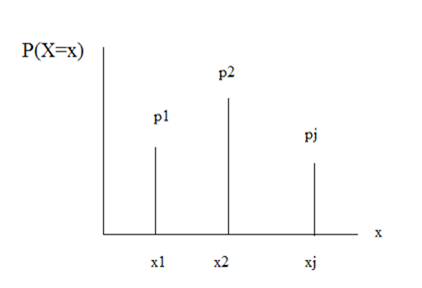
Possiamo utilizzare una rappresentazione tramite una tabella:
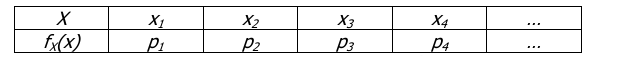
Esempio 1:
Nel caso dell'esperimento casuale di lancio di una moneta bilanciata con spazio campionario Ω costituito dai punti campionari Croce e Testa: Ω:= {C,T}
Si assume la variabile casuale X: Ω→R , che ad ogni punto dello spazio (croce e testa) associa uno ed un solo numero reale, ad esempio 0 a C ed 1 a T; simbolicamente abbiamo: X(C)=0; X(T)=1.
Abbiamo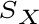 = {0,1} e la funzione di massa:
= {0,1} e la funzione di massa:
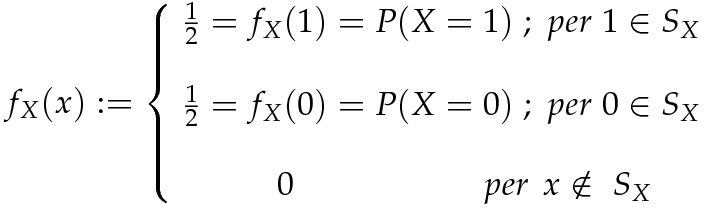
dunque osserviamo che la sua funzione di massa di probabilità è quella che è pari a per ogni punto appartenente al supporto: perché la
probabilità che X assuma valore 0 (cioè che esca croce)
è
per ogni punto appartenente al supporto: perché la
probabilità che X assuma valore 0 (cioè che esca croce)
è  e così anche la probabilità che X assuma valore 1 (esca testa).
Per ogni reale non appartenente al supporto ( cioè i valori
diversi da 0 ed 1) la funzione di massa di probabilità è
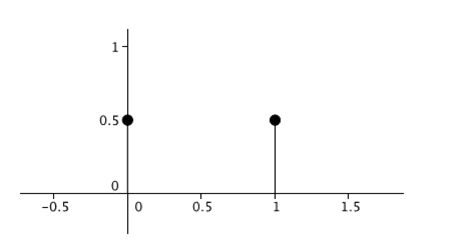
pari a zero. Il grafico:
e così anche la probabilità che X assuma valore 1 (esca testa).
Per ogni reale non appartenente al supporto ( cioè i valori
diversi da 0 ed 1) la funzione di massa di probabilità è
pari a zero. Il grafico:
Esempio 2 :
Esperimento: lancio di 2 monete Ω² = {(T,T);(T,C);(C,T);(C,C)}
Variabile casuale: X = numero totale degli esiti "testa"; X: Ω² → R ;
X è una variabile casuale discreta, i suoi possibili valori sono:
• 0 (se non si ottiene alcuna testa) X(C,C) =0
• 1 (se una delle due monete dà testa) X [(C,T),(T,C)]=1
• 2 (se entrambe le monete danno testa) X (T,T)=2
Abbiamo le probabilità:
• P(X=0)=P(C,C)=1/4
• P(X=1)=P((T,C) oppure (C,T))=2/4=1/2
• P(X=2)=P(T,T)=1/4
Abbiamo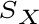 = {0,1,2} e la funzione di massa:
= {0,1,2} e la funzione di massa:
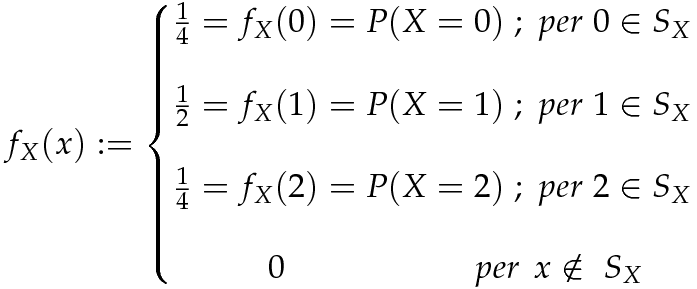
oppure in tabella:
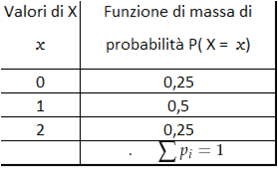
il grafico della funzione di massa (o di probabilità):
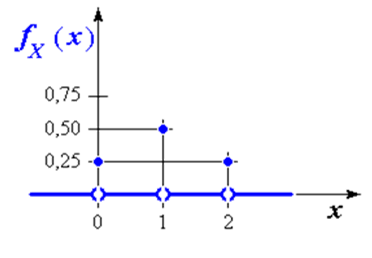
La distribuzione di probabilità è un modo di organizzare e quindi presentare in forma sintetica un insieme di dati. Le distribuzioni consentono di vedere come la variabile in esame si distribuisce nell'insieme analizzato.Esempio 3:

Consideriamo il lancio di due dadi. Ω è finito e quindi discreto. I risultati possibili (eventi elementari) sono infatti 36, mentre la variabile causale X="somma dei due punteggi" può assumere 11 possibili valori distinti : numeri interi compresi tra 2 e 12.
Vediamo nella seguente tabella la corrispondenza tra gli eventi di Ω ed i valori della variabile casuale X, nella prova "lancio di due dadi":
Primo dado
Secondo dado
Primo dado
Secondo dado
Primo dado
Secondo dado
Primo dado
Secondo dado
Primo dado
Secondo dado
Primo dado
Secondo dado
X
1
1
X=2
1
2
2
1
X=3
1
3
2
2
3
1
X=4
1
4
2
3
3
2
4
1
X=5
1
5
2
4
3
3
5
1
4
2
X=6
1
6
2
5
3
4
6
1
4
3
5
2
X=7
2
6
3
5
6
2
5
3
4
4
X=8
3
6
6
3
4
5
5
4
X=9
6
4
4
6
5
5
X=10
6
5
5
6
X=11
6
6
X=12
Poiché ogni evento elementare ha probabilità 1/36, dalla tabella si ricava, per esempio, che:
P(X=2)=P[(1;1)]=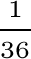 ; P(X=3)=P[(1;2)U (2;1)]=
; P(X=3)=P[(1;2)U (2;1)]= 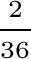 ...
...
In definitiva si ottiene la seguente distribuzione di probabilità:
X
2
3
4
5
6
7
8
9
10
11
12
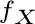 = P(X)
= P(X)1/36
2/36
3/36
4/36
5/36
6/36
5/36
4/36
3/36
2/36
1/36
- La distribuzione di probabilità di una variabile casuale discreta può essere rappresentata in modo grafico attraverso un istogramma di distribuzione di probabilità:
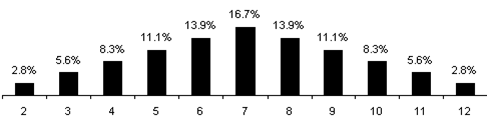
oppure: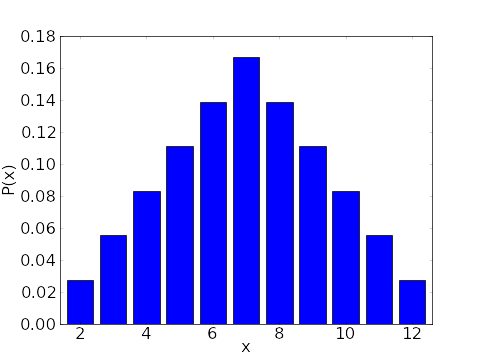
Nella rappresentazione con istogrammi è bene osservare che
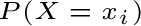 può essere
visualizzata mediante l’area del rettangolo la cui base ha
può essere
visualizzata mediante l’area del rettangolo la cui base ha 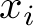 come punto medio.
Si noti anche che la somma delle aree dei
rettangoli è 1.
come punto medio.
Si noti anche che la somma delle aree dei
rettangoli è 1.La funzione di massa non può essere definita per le variabili casuali continue. Diamo una spiegazione basata su argomenti intuitivi. Una variabile casuale continua, come detto può assumere valori in un insieme continuo. Ora nel continuo, e questo vale anche se si prende un intervallo “piccolino”, ci sono tanti valori, assai più che nell’infinito numerabile. Se X avesse probabilità positiva, anche piccolissima, in ciascuno di questi valori, sommando tali probabilità otterremmo che la probabilità che X assuma un valore qualsiasi (evento certo) sarebbe infinito, contravvenendo ad una delle regole fondamentali della probabilità secondo le quali P(Ω) = 1. Quindi: primo, non ci possono essere più di un’infinità numerabile di punti con probabilità maggiore di 0; secondo, nel continuo P(X = x) = 0 in ogni x.
Pertanto nel continuo la funzione di massa non può essere definita e occorre un altro modo per vedere “cosa accade” sulle singole x: la funzione di densità.

 Torna all'Indice
Torna all'Indice  pagina successiva
pagina successiva