L’origine dei numeri.  1

 

 Le origini : l’assenza del numero.

 

     Le origini dell'uso dei numeri da parte dell'umanità naturalmente non sono documentate; le prime tracce di qualcosa che si suppone sia un conteggio risalgono a circa 30-35.000 anni fa, e sono costituite da ossa intagliate con tacche che si pensa indichino un qualche tipo di conteggio (giorni, animali ?). Il reperto più antico è l'osso di Lebombo, circa del 35000 a.C., un osso che riporta 29 tacche di tinte.Uno dei reperti più famosi è invece l'osso di Ishango: 

   

L'osso di Ishango

Anch'esso intagliato con tacche, sulle quali gli studiosi hanno fatto varie ipotesi, tra le quali quella che si tratti di un computo di giorni (un mese lunare).
Nella figura sotto un osso di renna intagliato risalente circa al 15.000 a.C.


Anche se non sappiamo datare con precisione quando siano apparsi dei primi esempi di “conteggio ” nella storia dell'umanità, una cosa è certa: 

I numeri non sono una parte “necessaria ” della cultura degli umani e delle loro capacità di descrivere l'ambiente.

Si può avere l'impressione che l'uso dei numeri sia qualcosa di immediato e "naturale", come e fosse innato, implicito nella struttura della nostra mente come la capacità di percepire il caldo e il freddo,o i colori; ma in effetti si può affermare con sicurezza che le cose non stanno affatto così: 

C'è stato un periodo in cui gli esseri umani non avevano il concetto di numero e del contare.


     La migliore prova di ciò è che esistono tuttora popolazioni che non hanno sviluppato il concetto di numero, e nei cui linguaggi le parole "uno", "due"e "molti" rappresentano tuttora le uniche grandezze utilizzate; si tratta, ad esempio, di tribù Zulu e Pigmei in Africa, di Aranda e Kamilarai in Australia, ed altre tribù isolate in Oceania od in Amazzonia.


   Ad esempio i Pirahã, una tribù di cacciatori-raccoglitori che vive lungo il fiume Maici, in Brasile, è stata recentemente studiata (un articolo su Science, di Peter Gordon della Columbia University è apparso nel 2004, vedi anche http://archiviostorico.corriere.it/2007); i Pirahã usano un sistema di conteggio chiamato  “uno-due-molti”.  In esso, la parola per “uno” si traduce come “circa uno” (simile al nostro “uno o due”), la parola per “due” significa “un po’ più di uno” (simile al nostro “pochi”), e poi c’è una parola per  “molti”.

   

Non è difficile costatare che esiste in ognuno di noi una percezione diretta del numero, una capacità immediata di distinguere insiemi con una quantità diversa di elementi, che non è legata al contare.  Considerate ad esempio gli insiemi di questa figura:

 

              

 

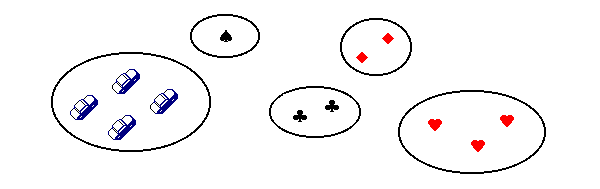
 Potete dire quanti sono gli elementi di ognuno di questi insiemi con una semplice occhiata: la percezione è immediata,  non avete bisogno di contare gli elementi degli insiemi.  

     La cosa è diversa con gli insiemi della figura seguente:


 

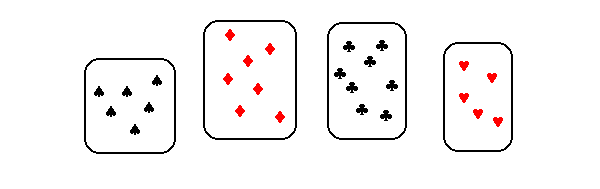
 In questo caso avete bisogno di contare in qualche modo gli elementi degli insiemi per dire quanti sono (lo potete fare raggruppandoli mentalmente a gruppi di due o tre, oppure contandoli uno ad uno, o in altro modo); che conclusione si può trarre da tutto ciò?  E' piuttosto semplice: 

La percezione immediata della quantità esiste, ma non supera il numero quattro!

 CURIOSITA’ :  Il corvo che contava fino a 4.  


Diversa è la situazione quando si passi ad analizzare la capacità di distinzione numerica come fatto culturale, guardando a come essa appare nel linguaggio, a come venga elaborata con parole e concetti: come notavamo all'inizio si ha quasi che il primo stadio di questa elaborazione è più arretrato della percezione immediata stessa, non andando oltre al "tre = tanti".


   Il fatto che "più di due = una moltitudine" sia stato uno stadio comune nell'evoluzione culturale delle popolazioni umane è testimoniato anche dalle sue tracce nelle lingue odierne: alcune lingue hanno fatto o fanno tuttora distinzione fra singolare, duale e plurale; hanno cioè parole distinte per il plurale di un sostantivo riguardante due oggetti (duale) e per quello riguardante tre o più. Si ha questa situazione in greco antico, nell'arabo e nello sloveno moderni. 

Altri esempi poi che testimoniano di una passata identità  "tre = molti" si trovano piuttosto facilmente:   

 

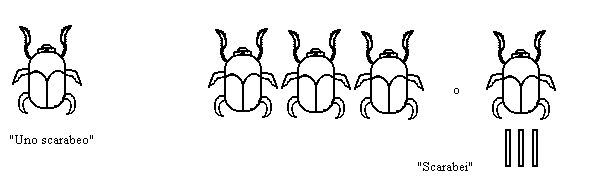
       Inoltre nei geroglifici egiziani la ripetizione per tre volte di un simbolo, o l'aggiungerci tre linee, significava sia "tre oggetti di quel tipo" che il plurale (indeterminato) di quella parola ; qualcosa di simile si trova anche nel cinese antico (tre alberi = foresta, tre uomini = folla). 

 

     

 

    Riassumendo, ciò che abbiamo notato mostra come il distinguere le quantità maggiori di due rappresenti una prima soglia, un primo stadio nell'evoluzione umana verso il concetto di numero, e come in questo stadio già il "tre" rappresenti delle moltitudini indistinte.

   

                                                                                                               

.