Geometria iperbolica >
Teoremi e definizioni >L'angolo di parallelismo
|
| L'ANGOLO
DI PARALLELISMO |
| 
|
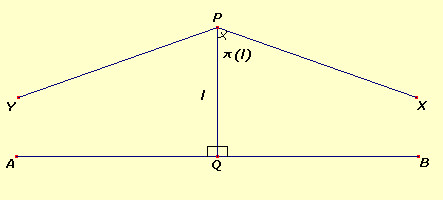
| Lobacevskij
chiamò l'angolo ^XPQ "angolo di parallelismo"
denotandolo col simbolo p(l),
dove l è la lunghezza di PQ.
|
Per il TEOREMA
2, |
| p(l)
= ^XPQ = ^YPQ < 90°.
|
La
grandezza dell'angolo rappresentato da
p(l) non dipende dal punto P o dalla
retta AB, ma soltanto dalla distanza l fra essi.
|
|
Se
R ed EF sono un qualunque
altro punto ed una qualunque altra retta separati dalla stessa
distanza l, ovvero se la perpendicolare RS
ha anch'essa lunghezza l, allora per il TEOREMA 10
si ha che ^VRS=^XPQ.
Se invece le distanze sono diverse,
anche gli angoli saranno diversi.
|
|
Se l1
è diverso da l2, allora p(l1)
è diverso da p(l2).
Infatti, se per assurdo supponiamo che sia
p(l1)
= p(l2),
otteniamo dal TEOREMA 11 che l1 = l2,
cioè una contraddizione.
Possiamo dunque concludere che fra le varie
distanze l ed i corrispondenti angoli di parallelismo
p(l)
c'è una corrispondenza biunivoca. |
| |
 |
 |