|
Geometria iperbolica > Teoremi e definizioni > L'area
di un triangolo iperbolico
|
L'AREA
DI UN TRIANGOLO IPERBOLICO
Quanto è più grande l'area
di un triangolo iperbolico, tanto minore è la somma
dei suoi angoli.
|
DEFINIZIONE |
| |
Il difetto
di un triangolo è ciò che manca alla
somma dei suoi angoli per raggiungere 180°. |
|
|
Il
difetto del triangolo ABC sarà
d =
180°-a-b-g |
|
I difetti
dei triangoli sono additivi, eccone un esempio:
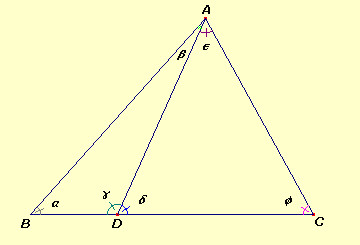
scegliamo un punto D a caso sul lato BC,
e tracciamo il segmento AD dividendo ABC
in due triangoli più piccoli. |
|
|
| Possiamo verificare immediatamente
che la somma dei difetti di questi due triangoli è
pari al difetto del triangolo somma.
Infatti: |
| |
d(ABD)+d(ADC) =
(180°-a-b-g)
+ (180°-d-e-f)
= |
| |
180°-a-b-g
+ 180°-d-e-f
=
180°-a-b-
(g + d)
+ 180°-e-f=
180°-a-b-
180° + 180°-e-f
=
180°-a-b-e-f
=
180°-a-
(b+e) -f
=
180°-a
- ^BAC -f
= d(ABC) |
|
| Si può dimostrare
che questo si verifica sempre, indipendentemente dal numero
di triangoli e dal modo in cui viene suddiviso ABC.
Naturalmente il fatto che i difetti siano
additivi è il motivo per cui i triangoli con area più
grande hanno la somma degli angoli minore.
Per chiarire le idee ragioniamo in un caso particolare:
Supponiamo che i triangoli
ABC e DEF abbiano aree differenti, e che
quella di ABC sia la maggiore;
|
|
supponiamo
inoltre di poter riportare una copia congruente di DEF
all'interno di ABC (questo è il caso particolare).
|
|
Tracciando alcune altre
linee possiamo suddividere completamente ABC in triangoli
più piccoli, uno dei quali è D'E'F'.
Il difetto di ABC sarà la somma dei difetti
dei triangoli in cui è stato suddiviso, perciò
sarà sicuramente maggiore del difetto di D'E'F' da
solo, e quindi la somma degli angoli di ABC è
minore di quella di D'E'F', ovvero del triangolo DEF
considerato nelle ipotesi. Abbiamo
ragionato su un caso particolare, non potremmo ripetere lo
stesso ragionamento con un triangolo DEF la cui forma
non potesse essere contenuta in ABC, tuttavia la
conclusione sarebbe ancora valida, ma richiederebbe una dimostrazione
molto più complicata.
|
TEOREMA 19 (generalizzazione
del TEOREMA 15) |
| |
Se la somma
dei tre angoli di un triangolo è uguale alla
somma dei tre angoli di un altro triangolo, allora i
due triangoli hanno la stessa area. |
Nell'ipotesi di questo teorema non viene
più richiesto che gli angoli siano a due a due uguali,
ma solo che la loro somma lo sia; corrispondentemente la tesi
è indebolita, infatti non possiamo più concludere
che i due triangoli sono congruenti ma solo che hanno la stessa
area. |
| |
 |
 |