|
Geometria iperbolica > Teoremi e definizioni > Il teorema
di Pitagora
|
IL
TEOREMA DI PITAGORA
Negli Elementi di Euclide
il teorema di Pitagora è il teorema 47, e viene dimostrato
utilizzando il V postulato; non ci stupisce dunque che tale
teorema non valga nella geometria iperbolica.
|

La proposizione I.47 dall'edizione degli
Elementi di Euclide del 1566
|
Il TEOREMA 13 ci porta
ad affermare che in un quadrilatero di Saccheri la sommità
è sempre più lunga della base.
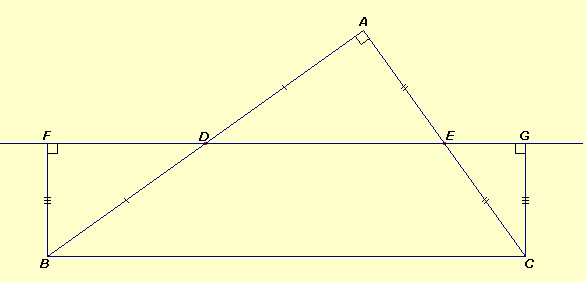
Consideriamo un triangolo rettangolo ABC e costruiamoci
sopra un quadrilatero di Saccheri come
in figura |
| 
|
| Se per assurdo
il teorema di Pitagora fosse valido, potremmo applicarlo ai
triangoli rettangoli ABC e ADE, ottenendo
le relazioni: |
BC2=AB2+AC2 |
[1] |
DE2=AD2+AE2 |
[2] |
Poiché
AD=1/2 AB e AE=1/2 AC,
possiamo riscrivere l'equazione [2] come |
DE2=(1/2
AB)2+(1/2 AC)2 =1/4
AB2+1/4 AC2=1/4 (AB2+AC2). |
| Per l'equazione [1], 1/4
(AB2+AC2) = 1/4 BC2,
quindi |
DE2=1/4
BC2ovvero DE=1/2 BC. |
Ma DE=1/2
FG, quindi otteniamo che la sommità BC
è uguale alla base FG.
Questa è una contraddizione. |
| |
|
 |
 |