|
Geometria iperbolica > Esercizi dinamici > Applet Non
Euclid
|
| Esercizi
dinamici con l'applet Non Euclid |
| |
NonEuclid
permette di studiare due modelli di geometria iperbolica piana
noti rispettivamente come modello del disco e modello del
semipiano di Poincaré. E' possibile scegliere una delle
due opzioni cliccando nel menu dell'applet: Visualizza >
modello iperbolico > disco/semipiano.
In questa trattazione è stato descritto il modello
del piano di Poincaré, grazie all'applet Non Euclid
è ora possibile sperimentare ciò che finora
si è solo immaginato.
La grande circonferenza che compare all'avvio di NonEuclid
è la circonferenza limite. Essa delimita l'area dello
schermo in cui si possono eseguire costruzioni geometriche
e individua l'intero piano iperbolico.
E' possibile ora costruire oggetti e verificarne le proprietà,
per familiarizzare con questo nuovo tipo di strana geometria! |
| |
Uno degli
esercizi di maggiore interesse da svolgere con NonEuclid consiste
nel partire da alcuni enunciati di teoremi validi in geometria
euclidea e di vedere quali di questi enunciati rimangono validi
anche in geometria iperbolica.
|
| L'utilizzo dell'applet
è molto semplice, i comandi sono chiari e precisi:
attraverso il menu Costruzioni è possibile disegnare
punti, segmenti, rette, circonferenze, semirette, perpendicolari,
bisettrici ecc.
E' possibile inoltre inserire etichette, scegliere il colore
dei diversi oggetti, spostare i punti disegnati, misurare
lunghezze, distanze ed angoli.
Per iniziare a lavorare con Non
Euclid clicca su questo bottone.
|
Esercizio guidato: verificare che la somma degli
angoli interni di un triangolo vale meno di 180°.
Il triangolo iperbolico di figura
si costruisce eseguendo i seguenti passaggi:
- Seleziona l'opzione
"Segmento" dal menu "Costruzioni".
- Sposta il mouse all'interno della circonferenza limite.
- Clicca con il mouse in un punto interno alla circonferenza
limite. Così viene rappresentato sullo schermo il punto
A.
- Clicca con il mouse in un secondo punto interno alla circonferenza
limite. Così compare sullo schermo il punto B e viene
disegnato il segmento iperbolico che congiunge A con B.
- Clicca con il mouse in corrispondenza del punto B.
- Clicca con il mouse in un terzo punto interno alla circonferenza
limite. Così viene rappresentato sullo schermo il punto
C e viene disegnato il segmento iperbolico che congiunge B
con C.
- Clicca con il mouse in corrispondenza dei punti C e A. Così
viene disegnato il segmento iperbolico che congiunge C con
A ed il triangolo iperbolico è costruito.
- A questo punto, aprendo il Menu "Misure" e selezionando
l'opzione "Misura Triangolo" è possibile
ottenere le lunghezze dei lati del triangolo e le misure dei
suoi angoli interni.
Osserviamo che la somma dei tre angoli interni del triangolo
è MINORE DI 180°.
Esercizio
guidato: osservare che in geometria iperbolica la
formula Area = (base x altezza)/2 offre tre risposte diverse
in relazione al lato che si sceglie come base del triangolo.
|
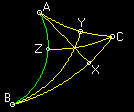 |
Il
triangolo ABC è scaleno. I segmenti AX, BY e CZ individuano
le tre altezze del triangolo ABC. Osserviamo che, come in
geometria euclidea le tre altezze si intersecano in un unico
punto.
Misurando lati e angoli del triangolo otteniamo:
|
|
lunghezza della base AB = 3,3 altezza
CZ = 1,1
lunghezza della base BC = 3,0, altezza AX = 1,9
lunghezza della base AC = 2,1 altezza BY = 2,5
angolo AXB = angolo AXC = 90°
angolo BYA = angolo BYC = 90°
angolo CZA = angolo CZB = 90° |
Se ora proviamo a calcolare l'area del triangolo usando
la formula A=bh/2 troviamo che il numero ABxCZ/2 è
DIVERSO da BCxAX/2 e da ACxBY/2.
Una formula che da tre risposte diverse in relazione al
lato che si sceglie come base del triangolo risulta chiaramente
inaccettabile, per cui A=bh/2 non può essere considerata
una formula valida per il calcolo dell'area di un triangolo
iperbolico.
|
Esercizi
proposti: |
- Vedere se in un triangolo il
lato maggiore è sempre opposto all'angolo di ampiezza
maggiore.
- Vedere se le tre altezze di un triangolo si intersecano
in un unico punto detto ortocentro (per costruire l'altezza
di un triangolo si utilizzi il comando "Perpendicolare"
nel menu "Costruzioni") .
- Vedere se in un triangolo il prodotto "base per altezza"
assume lo stesso valore indipendentemente dal lato di base
scelto.
- Verificare che non vale il Teorema di Pitagora: dato un
triangolo rettangolo la somma dei quadrati delle lunghezze
dei cateti non è uguale al quadrato della lunghezza
dell'ipotenusa.
- Vedere se icriteri di congruenza
dei triangoli validi in geometria euclidea continuano a
valere in geometria iperbolica.
- Vedere se è'
possibile costruire un quadrilatero regolare.
- Vedere se le
diagonali di un quadrilatero regolare sono tra loro perpendicolari.
- Costruendo diversi triangoli
iperbolici e misurando il loro difetto verificare che se
il triangolo è "piccolo" anche il suo difetto
risulta tale per cui la somma degli angoli interni del triangolo
si avvicina al valore 180°. [Più precisamente
si verifica che al tendere a zero del perimetro del triangolo
la somma degli angoli interni tende al valore 180°].
Al contrario per triangoli "grandi"
il difetto risulta a sua volta "grande". [Al tendere
all'infinito delle lunghezze dei lati del triangolo gli
angoli tendono a zero e il difetto si avvicina al valore
massimo di 180°].
- Verificare che il difetto è
additivo.
|
| |
 Modello di Poincaré
Modello di Poincaré |
 Geometria iperbolica
Geometria iperbolica |
 Arte iperbolica
Arte iperbolica |
|