|
Geometria iperbolica > I modelli
della geometria iperbolica > Beltrami
|
La "traduzione"
si ottiene interpretando la superficie pseudosferica come piano
di Lobacevskji, le rette di questo piano sono le geodetiche
della superficie.
Così la pseudosfera costituisce un modello della geometria
iperbolica.
|
 |
superficie pseudosferica
|
regione di piano non
euclideo |
| punto della superficie |
punto del piano |
| geodetica |
retta del piano |
| arco di geodetica |
segmento del piano |
| due punti determinano una geodetica
|
due punti determinano una retta
del piano |
| per un punto esterno
a una geodetica passano infinite geodetiche che non si
incontrano con quella data |
per un punto
esterno a una retta passano infinite rette parallele
alla retta data |
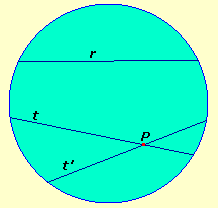
Un disegno nel piano
del modello di Beltrami schematicamente illustrato qui
sopra: un disco (bordo escluso) nel piano usuale, in cui
le geodetiche appaiono come porzioni di rette
Per il punto P esterno alla retta r passano almeno
due rette, t e t', che non incontrano
la retta r.
Per interpretare correttamente il modello è
però necessario rendersi conto che:
- La misura delle distanze e degli angoli non è
quella usuale; le distanze divengono tanto più
grandi, e gli angoli più piccoli, rispetto a quelli
usuali, quanto più ci si avvicina al bordo del
disco.
- Le geodetiche sono indefinitamente estese e hanno lunghezza
infinita.
Nel modello tutti gli assiomi della geometria euclidea
sono soddisfatti, tranne quello delle parallele, che nel
modello sono infinite. |
|
Questo
risultato assicura una non contraddittorietà relativa
di questa geometria; infatti, se la geometria iperbolica fosse
contraddittoria, vi sarebbe una contraddizione nella geometria
della pseudosfera, la quale, a sua volta, è stata definita
mediante concetti di geometria euclidea. Pertanto vi sarebbe
una contraddizione nella geometria euclidea.
E' bene sottolineare
che le considerazioni relative alla geometria di una superficie,
dato il loro carattere locale, non sono conclusive dal punto
di vista delle questioni di non contraddittorietà delle
nuove geometrie. Queste considerazioni valgono infatti solo
nell'intorno di ogni punto, quindi in regioni limitate, e
non sull'intera superficie.
Se pensiamo per esempio ad una geometria di piccole regioni
di una superficie cilindrica, possiamo pensarla coincidente
con la geometria di una regione del piano (basta srotolare
il cilindro), ma non possiamo dire lo stesso per l'intera
superficie cilindrica, in cui le geodetiche sono chiuse (circonferenze),e
altre si incontrano in infiniti punti distinti (le eliche
cilindriche).
Lo stesso ragionamento vale anche per altre superfici.
|
Il punto
più debole dell'argomentazione di Beltrami sta dunque
nel fatto che il modello ha valore locale e non può
rappresentare globalmente la geometria non euclidea. Infatti,
tra le infinite forme che una superficie pseudosferica può
assumere si conosce l'espressione analitica solo di qualche
caso particolare. Beltrami l'aveva ottenuta dalla rotazione
di una trattrice, e questa curva ha il difetto di avere un
punto cuspidale, che ruotando dà origine a un cerchio
di punti singolari della superficie: la superficie ottenuta
dalla rotazione della trattrice quindi non è regolare
e non può rappresentare interamente il piano non euclideo.
Il problema è allora se tra tutte le superfici, delle
quali non si conosce l'espressione analitica, ne esiste almeno
una che sia regolare.
Beltrami ne era convinto ma non riuscì a provarlo.
Il 13 marzo 1869 scriveva a Hoüel, un suo amico matematico
francese:
|
| |
"Ho
avuto nel frattempo un'idea bizzarra,
che voglio comunicarle in quanto potrebbe essere per voi
più facile che a me metterla in atto. Ho voluto
tentare di costruire materialmente la superficie pseudosferica
sulla quale si realizzano i teoremi della geometria non
euclidea". |
|
|
Il modello materiale costruito
in cartone aveva il diametro di 1,04 m; oggi è custodito
presso il dipartimento di matematica dell'Università
di Pavia. Per la sua forma, un giornale satirico dell'epoca
battezzò l'oggetto "cuffia della nonna",
tanto che ancora oggi il modello è anche detto "cuffia
di Beltrami".
|
|
|
L'idea
di Beltrami fu dunque quella di costruire un modello di geometria
non euclidea prendendo come spazio una superficie di curvatura
costante negativa e come rette le sue geodetiche. Una seria
difficoltà fu che nello spazio ordinario non ci sono
superfici di curvatura costante negativa le cui geodetiche
si possano estendere indefinitamente.
Nel 1901 Hilbert dimostra rigorosamente che il modello descritto
da Beltrami ha un valore esclusivamente locale e non può
essere accettato come prova matematica.
E in un teorema afferma che:
non esiste alcuna superficie regolare su cui valga nella
sua completezza la geometria di Lobacesvkji e Bolyai.
A questo si aggiunge il teorema di Liebmann:
Una superficie su cui valesse nella sua completezza la
geometria di Riemann deve essere chiusa e l'unica superficie
chiusa a curvatura costante positiva è la sfera.
D'altra parte le geodetiche della sfera, che sono i cerchi
massimi, si incontrano sempre in due punti opposti, per cui:
Nello spazio euclideo non esiste alcuna superficie che
soddisfi integralmente le geometrie non euclidee.
|
Il modello
di Beltrami, pur non essendo un modello rigoroso, è
molto importante da un punto di vista storico: è stato
il primo di diversi modelli che hanno iniziato a far cadere
le opposizioni preconcette verso i nuovi sistemi geometrici
e ha fornito la chiave per interpretare le nuove geometrie
non euclidee.
Per la conoscenza
di un altro modello della geometria iperbolica si veda il
modello
di Poincaré.
|
 |
 Modello di Poincaré
Modello di Poincaré |
|
|