Geometria iperbolica > I modelli della geometria iperbolica > Beltrami
EUGENIO BELTRAMI ED IL SUO MODELLO PER LA GEOMETRIA IPERBOLICA

Il matematico Eugenio Beltrami (1835-1900), che si occupò attivamente di geometria differenziale, presentò il primo modello di geometria non euclidea. In una memoria del 1866, Risoluzione del problema di riportare i punti di una superficie sopra un piano in modo che le linee geodetiche vengano rappresentate su rette, pose le basi che gli consentirono, due anni dopo, di presentare un modello della geometria iperbolica. Fece questo nel Saggio di interpretazione della geometria non euclidea (1868), un suo manoscritto redatto qualche anno prima e messo da parte per paura delle aspre critiche che coinvolgevano chi si occupava di geometrie dette 'astrali' o 'da manicomio'. Il suo Saggio di interpretazione della geometria non euclidea segna un punto di svolta nella ricerca geometrica su questo millenario problema.


Beltrami aveva trovato un modello per la geometria di Lobacevskji, ossia aveva trovato all'interno della geometria euclidea, una superficie di rotazione, la pseudosfera, che poteva essere interpretata come un modello euclideo di geometria non euclidea. In questo modo dimostrava che la geometria di Lobacevskji ha lo stesso diritto logico-matematico della classica geometria di Euclide.
Consideriamo una linea piana detta trattice o curva delle tangenti costanti (introdotta nel 1939 da Ferdinand Minding), definita come quella curva per la quale è costante il segmento di tangente compreso tra il punto di contatto e una retta fissa del piano. Assumiamo come tale retta fissa l'asse x. In questo caso, detta k la lunghezza costante del segmento di tangente, si può dimostrare che l'equazione della trattice è

Se facciamo ruotare la trattice intorno all'asse x nello spazio, questa genera una superficie di rotazione che prende il nome di pseudosfera, perché ha una curvatura costante come quella di una sfera, ma di segno negativo: -1/k2.
Beltrami dimostrò che, applicando l'interpretazione dei concetti della geometria del piano ai concetti della geometria delle superfici, si trova che alla pseudosfera compete una geometria che soddisfa, almeno in regioni limitate di piano, gli assiomi della geometria iperbolica.

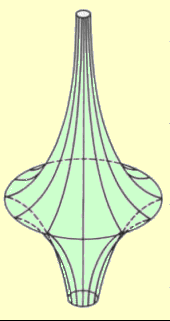pseudosfera

 
Per capire come avviene questa "traduzione" occorre introdurre la nozione di geodetica.
Nel piano il percorso più breve che unisce due punti si trova sulla retta passante per i due punti. Estendendo questo concetto alle superfici, il percorso più breve che unisce due punti della superficie si trova su di una linea, generalmente curva, detta geodetica. Per esempio, dovendosi muovere sulla superficie di una sfera, il percorso più breve non è quello rettilineo, perché non esistono percorsi di questo tipo, ma è l'arco di cerchio massimo, che in questo caso è una geodetica.

Un altro modo, del tutto equivalente, di definire le geodetiche, è come le traiettorie descritte da un punto materiale che si muova, senza attrito e non soggetto a forze esterne, sulla superficie stessa. La figura seguente mostra due geodetiche tracciate su una superficie a forma di coppa svasata.