- 1)
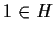 ;
;
- 2)
-
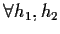
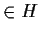 ,
,
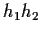
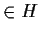 ;
;
- 3)
-
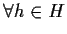 ,
,
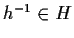 .
.
Osservazione 2
Se ![]() è un sottoinsieme non vuoto di un gruppo
è un sottoinsieme non vuoto di un gruppo ![]() ,
la condizione
,
la condizione ![]() della definizione 1 può essere dedotta
dalle condizioni
della definizione 1 può essere dedotta
dalle condizioni ![]() e
e ![]() :
se
:
se ![]() ,
,
![]() .
.
La condizione ![]() della definizione 1 si esprime dicendo
che
della definizione 1 si esprime dicendo
che ![]() è chiuso rispetto al prodotto.
è chiuso rispetto al prodotto.
