Esempio 14
Sia
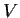
uno spazio vettoriale hermitiano, cioè un
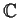
-spazio vettoriale su cui è definito un prodotto
hermitiano
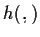
.
L'insieme
è un sottogruppo di
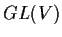
,
detto
gruppo
unitario di 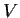
. Infatti, ricordando che
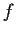
è unitario se
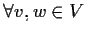
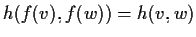
,
si ha:
-
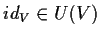 ;
;
- se
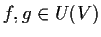 ,
,
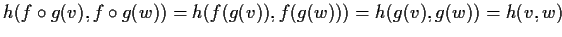 ,
cioè
,
cioè
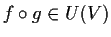 ;
;
- se
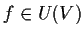 ,
,
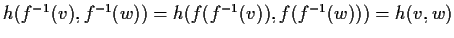 ,
dunque
,
dunque
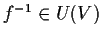 .
.
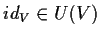 ;
;
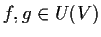 ,
,
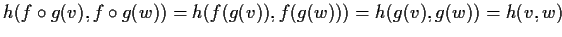 ,
cioè
,
cioè
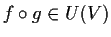 ;
;
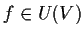 ,
,
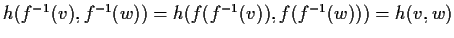 ,
dunque
,
dunque
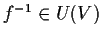 .
.