condizione necessaria e sufficiente affinchè due applicazioni lineari inducano lo stesso morfismo proiettivo

12 PROPOSIZIONE Due applicazioni lineari iniettive $\varphi,\psi:\mathbf{V} \longrightarrow \mathbf{V'}$ inducono lo stesso morfismo proiettivo $f:\mathbf{P(V)} \longrightarrow \mathbf{P(V')}$ se e solo se esiste $\lambda \in \mathrm{K}^{\ast}$ tale che $\psi=\lambda \varphi.$
Quindi l'applicazione che induce un dato morfismo proiettivo è individuata solo a meno di un fattore di proporzionalità non nullo.

Dimostrazione
Sia $\psi=\lambda \varphi$ con $\lambda \in \mathrm{K}^{\ast}.$
Allora $[\varphi (\mathbf{v}) ]=[\lambda \varphi (\mathbf{v}) ]=[\psi (\mathbf{v}) ].$ Quindi $\varphi$ e $\psi$ inducono lo stesso morfismo proiettivo

$\begin{displaymath}\begin{array}{cccl} f: & \mathbf{P(V)} & \longrightarrow & \... ...psto & [\varphi (\mathbf{v}) ]=[\psi (\mathbf{v}) ] \end{array}\end{displaymath}$

Viceversa, supponiamo che $\varphi$ e $\psi$ inducano lo stesso isomorfismo proiettivo; possiamo supporre che

sia un isomorfismo, perché se non lo è lavoriamo con $\tilde{f}:\mathbf{P(V)} \longrightarrow \mathbf{P}(\mathrm{Im}(\varphi)).$ Quindi supponiamo $\varphi$ e $\psi$ isomorfismi vettoriali, e $[\varphi (\mathbf{v}) ]=[\psi (\mathbf{v}) ]$ per ogni $\mathbf{v} \in \mathbf{V}\setminus \{ \mathbf{0}\}.$ Questo significa che per ogni $\mathbf{v} \in \mathbf{V}\setminus \{ \mathbf{0}\}$ esiste $\lambda (\mathbf{v}) \in \mathrm{K}^{\ast}$ tale che $\psi (\mathbf{v}) =\lambda (\mathbf{v}) \varphi (\mathbf{v}),$ cioè che per ogni $\mathbf{v} \in \mathbf{V}\setminus \{ \mathbf{0}\}$ esiste $\lambda (\mathbf{v}) \in \mathrm{K}^{\ast}$ tale che $\varphi^{-1} (\psi (\mathbf{v}))=\varphi^{-1} (\lambda (\mathbf{v}) \varphi (\mathbf{v})).$ Ma $\varphi^{-1}$ è lineare, quindi $\varphi^{-1} (\lambda (\mathbf{v}) \varphi (\mathbf{v}))=\lambda (\mathbf{v})\varphi^{-1} (\varphi (\mathbf{v}))=\lambda (\mathbf{v}) \mathbf{v};$ pertanto ogni $\mathbf{v} \in \mathbf{V}\setminus \{ \mathbf{0}\}$ è un autovettore di $\varphi^{-1} \circ \psi.$
Sia ora $\mathcal{B} = (\mathbf{v_0}, \ldots, \mathbf{v_n})$ una base di $\mathbf{V}.$ Poniamo $\lambda (\mathbf{v_i})=\lambda_i$ per $i=0,\ldots,n.$ Siano $0 \leq i,j \leq n$ due indici distinti, e sia $\mathbf{v}=\mathbf{v_i}+\mathbf{v_j}.$
Allora esiste $\lambda (\mathbf{v}) \in \mathrm{K}^{\ast}$ tale che $\varphi^{-1} \circ \psi (\mathbf{v})=\lambda (\mathbf{v}) \mathbf{v}=\lambda (\mathbf{v}) \mathbf{v_i}+\lambda (\mathbf{v}) \mathbf{v_j}.$
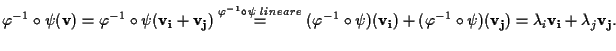D'altra parte si ha: $\varphi^{-1} \circ \psi (\mathbf{v})=\varphi^{-1} \circ \psi (\mathbf{v_i}+\mat... ...^{-1} \circ \psi) (\mathbf{v_j})=\lambda_i \mathbf{v_i}+\lambda_j \mathbf{v_j}.$ Quindi

$\begin{displaymath}(\lambda (\mathbf{v})-\lambda_i)\mathbf{v_i}+(\lambda (\mathbf{v})-\lambda_j)\mathbf{v_j}=0.\end{displaymath}$

Pertanto, per l'indipendenza lineare di $\mathbf{v_i}$ e $\mathbf{v_j},$ deduciamo che $\lambda_i=\lambda_j=\lambda (\mathbf{v}).$
In conclusione: $\lambda_0=\lambda_1=\cdots=\lambda_n=\lambda.$ Quindi $\varphi^{-1} \circ \psi =\lambda \mathsf{id}_{\mathbf{V}},$ cioè $\psi (\mathbf{v})=\lambda \varphi (\mathbf{v})$ per ogni $\mathbf{v} \in \mathbf{V}.$