9 PROPOSIZIONE
Se
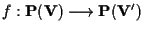
e
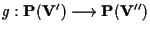
sono morfismi proiettivi indotti dalle
applicazioni lineari iniettive
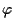
e
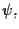
allora
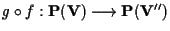
è un morfismo proiettivo
indotto da
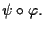
Dimostrazione
L'applicazione
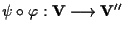 è
lineare e iniettiva, in quanto composizione di due applicazioni lineari e
iniettive; quindi induce il morfismo proiettivo
è
lineare e iniettiva, in quanto composizione di due applicazioni lineari e
iniettive; quindi induce il morfismo proiettivo
Si vede subito che
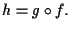
10 OSSERVAZIONE
Siano
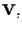
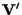
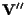
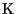
-spazi vettoriali di dimensione finita. Allora:
a)
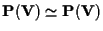
tramite l'isomorfismo
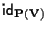
indotto da
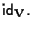 b
b) Se
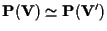
e
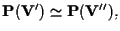
allora
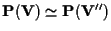
(ciò segue da
proposizione 9).
11 PROPOSIZIONE
 a
a) Due spazi proiettivi
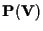
e
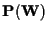
con
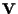
e
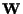
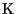
-spazi vettoriali sono isomorfi se e solo se
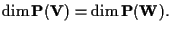 b
b) Ogni spazio proiettivo
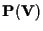
con
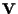
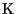
-spazio vettoriale di dimensione
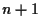
è isomorfo a
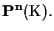
Dimostrazione
Segue immediatamente dal fatto che due
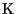 -spazi vettoriali di dimensione finita sono isomorfi se e solo se hanno la stessa dimensione.
-spazi vettoriali di dimensione finita sono isomorfi se e solo se hanno la stessa dimensione.
![]() è
lineare e iniettiva, in quanto composizione di due applicazioni lineari e
iniettive; quindi induce il morfismo proiettivo
è
lineare e iniettiva, in quanto composizione di due applicazioni lineari e
iniettive; quindi induce il morfismo proiettivo
![]()
![]() -spazi vettoriali di dimensione finita sono isomorfi se e solo se hanno la stessa dimensione.
-spazi vettoriali di dimensione finita sono isomorfi se e solo se hanno la stessa dimensione.



