4 OSSERVAZIONE
Se
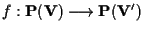
è un
isomorfismo indotto da
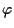
,
allora
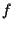
è invertibile, e l'inversa,
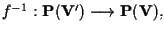
è un isomorfismo, indotto da
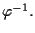
6 ESEMPIO
Consideriamo l'applicazione lineare
Tale applicazione è un isomorfismo, infatti
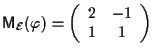 ha determinante non nullo.
ha determinante non nullo.
Quindi 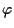 induce la proiettività
induce la proiettività
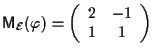 ha determinante non nullo.
ha determinante non nullo. ![]() induce la proiettività
induce la proiettività



