15 DEFINIZIONE
Siano
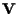
e
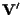
spazi vettoriali di dimensioni rispettivamente
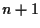
ed
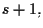
con basi rispettivamente
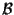
e
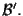
Sia
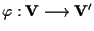
un'applicazione lineare e iniettiva, siano
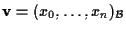
e
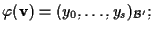
ricordiamo che le equazioni di
rispetto alle basi
e
sono date da
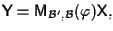
dove
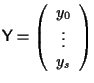
e
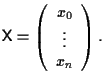
Sia
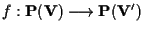
il morfismo proiettivo indotto da
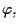
e siano infine
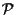
e
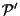
i riferimenti proiettivi rispettivamente su
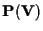
e
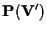
associati alle basi
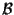
e
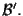
Le equazioni
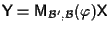
sono dette
equazioni di 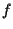 rispetto ai riferimenti
rispetto ai riferimenti
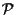
e
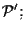
ma attenzione: se
![$P=[a_0,\ldots,a_n]_{\mathcal{P}}$](img44.gif)
e
![$f(P)=[b_0,\ldots,b_s]_{\mathcal{P'}},$](img45.gif)
possiamo solo dire che esiste
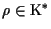
tale che
Si dice anche che la matrice
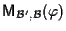 rappresenta
rappresenta 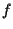 rispetto ai riferimenti proiettivi
rispetto ai riferimenti proiettivi
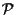 e
e
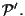
16 OSSERVAZIONE
Nelle medesime ipotesi della proposizione precedente, una matrice
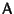
rappresenta
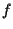
rispetto ai riferimenti proiettivi
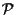
e
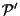
se e solo se esiste
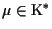
tale che
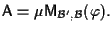
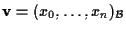 e
e
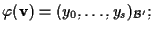 ricordiamo che le equazioni di
ricordiamo che le equazioni di
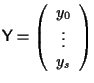 e
e
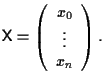 Sia
Sia
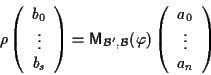
![]() rappresenta
rappresenta ![]() rispetto ai riferimenti proiettivi
rispetto ai riferimenti proiettivi
![]() e
e
![]()
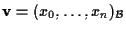 e
e
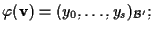 ricordiamo che le equazioni di
ricordiamo che le equazioni di
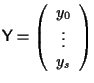 e
e
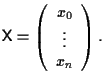 Sia
Sia
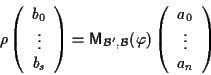
![]() rappresenta
rappresenta ![]() rispetto ai riferimenti proiettivi
rispetto ai riferimenti proiettivi
![]() e
e
![]()



