osservazione

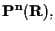
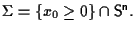
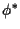
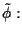
2 OSSERVAZIONE Un modello piú semplice per $\mathbf{P^n(R)},$ dedotto dal precedente, si può costruire nella maniera seguente. Sia $\Sigma =\{ x_0 \geq 0\} \cap \mathsf{S^n}.$ Possiamo considerare l'applicazione biunivoca $\phi^{\ast}$ indotta da $\tilde{\phi}:$

$\begin{displaymath}\phi^{\ast}:\Sigma /_{\mathcal{R}} \longrightarrow \mathbf{P^n(R)}.\end{displaymath}$

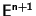
Le rette vettoriali di $\mathsf{E^{n+1}}$ che non sono contenute nell'iperpiano

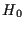
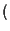
di equazione

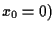
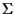
incontrano $\Sigma$ in un solo punto.
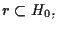
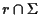
Se invece $r \subset H_0,$ allora $r \cap \Sigma$ è una coppia di punti antipodali. Quindi le classi di equivalenza sono fatte cosí:

$\begin{displaymath}\mbox{se}\; P \in \{ x_0>0\},\; \mbox{allora} \; [P]_{\mathcal{R}} =\{ P\},\end{displaymath}$

$\begin{displaymath}\mbox{se}\; P \in \{ x_0=0\},\; \mbox{allora} \; [P]_{\mathcal{R}} =\{ P, -P\}.\end{displaymath}$

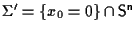
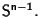
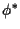
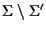
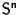
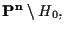
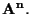
Sia ora $\Sigma'=\{ x_0=0\} \cap \mathsf{S^n}$ il bordo della calotta, che è $\mathsf{S^{n-1}}.$ L'applicazione $\phi^{\ast}$ induce allora una biezione di $\Sigma \setminus \Sigma'$ (che è la calotta superiore della sfera $\mathsf{S^n}$ senza il bordo) su $\mathbf{P^n} \setminus H_0,$ che è identificabile ad $\mathbf{A^n}.$
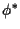
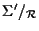
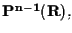
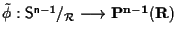
Inoltre $\phi^{\ast}$ induce una biezione tra $\Sigma'/_{\mathcal{R}}$ e $\mathbf{P^{n-1}(R)},$ che non è altro che la $\tilde{\phi}:\mathsf{S^{n-1}}/_{\mathcal{R}} \longrightarrow \mathbf{P^{n-1}(R)}$ definita in osservazione 1.