1 OSSERVAZIONE   Identifichiamo $\mathbf{P^n(R)}$ con l'insieme i cui elementi sono le rette per l'origine di $\mathsf{E^{n+1}}$ (che è l'$(n+1)$-spazio euclideo numerico).
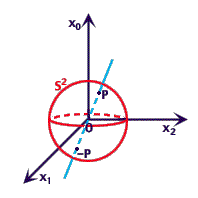
Consideriamo la sfera $\mathsf{S^n} \subset \mathsf{E^{n+1}},$ di centro l'origine $O$ e raggio $1.$ Tale sfera è l'insieme $\{ (x_0,\ldots,x_n) \in \mathsf{E^{n+1}}: \mathrm{d}((x_0,\ldots,x_n),(0,\ldots,0))=1 \},$ dove $\mathrm{d}$ è la distanza euclidea, cioè $\mathsf{S^n}=\{ (x_0,\ldots,x_n) \in \mathsf{E^{n+1}}:x_0^2+x_1^2+\cdots+x_n^2=1 \}.$

Definiamo un'applicazione

\begin{displaymath}\begin{array}{cccl} \phi: & \mathsf{S^n} & \longrightarrow &... ...& \mbox{retta per l'origine che contiene}\; P=[P-O] \end{array}\end{displaymath}

Poiché ogni retta passante per l'origine incontra $\mathsf{S^n}$ in due punti simmetrici rispetto ad essa $($che denotiamo con $\{ P,-P\}),$ detti antipodali o diametralmente opposti, l'applicazione $\phi$ è suriettiva, e tale che $\phi^{-1} ([\mathbf{v}])$ consiste di due punti per ogni $[\mathbf{v}] \in \mathbf{P^n}.$
Risulta cioè: $\phi (P)=\phi (-P) =[\mathbf{v} ]$ e $\phi^{-1} ([\mathbf{v} ])=<\mathbf{v}> \cap \mathsf{S^n}=\{ P,-P\}.$
La funzione $\phi$ fa dunque corrispondere biunivocamente $\mathbf{P^n(R)}$ all'insieme i cui elementi sono le coppie di punti antipodali $\{ P,-P\}$ di $\mathsf{S^n}.$ Pertanto, denotando con $\mathcal{R}$ la relazione antipodale $($cioè: $P\; \mathcal{R} \; Q$ se e solo se $P=Q$ oppure $P=-Q),$ $\phi$ induce un'applicazione biunivoca

\begin{displaymath}\tilde{\phi}:\mathsf{S^n}/_{\mathcal{R}} \longrightarrow \mathbf{P^n(R)}.\end{displaymath}

PAGINA PRECEDENTE INIZIO PAGINA PAGINA SUCCESSIVA PERCORSO SUGGERITO