27 ESEMPIO
Due rette distinte
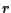
ed
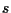
in un piano proiettivo si incontrano sempre, ed
esattamente in un punto. Infatti:
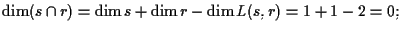
questo vale perché
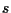
ed
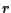
sono due rette distinte
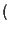
quindi
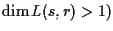
e siamo in un piano, pertanto
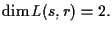
28 ESEMPIO
In uno spazio proiettivo
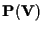
di dimensione tre, invece, può
accadere che due rette
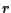
ed
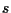
siano sghembe
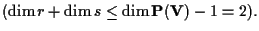
Questo effettivamente accade: se consideriamo per esempio due piani vettoriali in
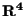
che si incontrano solo nel punto
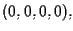
allora i loro proiettivizzati in
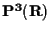
sono due rette sghembe.
Una retta
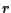
e un piano
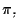
però, si incontrano sempre
infatti, per il
corollario 25,
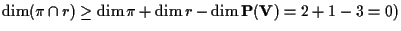
in
due modi:
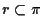
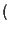
questo vale se e solo se
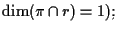
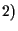
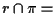
un unico punto
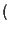
questo vale se e solo se
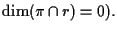
Infine, due piani distinti
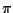
e
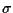
in uno spazio proiettivo di
dimensione tre hanno sempre in comune una retta, infatti
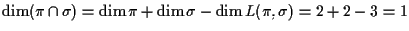
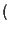
la dimensione di
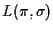
è uguale a
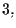
poiché
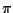
e
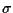
sono distinti
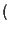
quindi
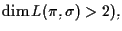
e siamo in uno spazio proiettivo tridimensionale
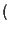
quindi
29 ESEMPIO
In uno spazio proiettivo
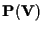
di dimensione 4 due rette
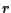
ed
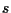
,
una retta
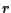
e un piano
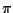
possono essere sghembi
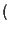
infatti
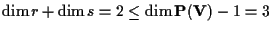
e
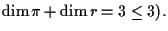
Questo accade effettivamente: basta considerare per esempio i proiettivizzati di due piani vettoriali, rispettivamente di un piano e di un sottospazio tridimensionale, che in
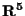
si incontrano solo nel punto
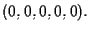
Due piani
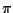
e
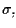
invece, sono sempre incidenti
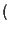
infatti
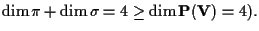
Vediamo in che modo possono
incontrarsi
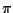
e
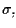
sempre servendoci della formula di Grassmann
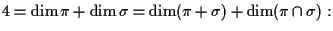
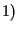
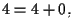
cioè
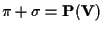
e
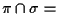
un punto (è il caso dei proiettivizzati di due sottospazi vettoriali di dimensione 3 in
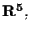
la cui somma è
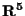
e la cui intersezione è una retta);
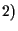
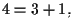
cioè
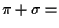
un iperpiano e
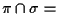
una retta (è il caso dei proiettivizzati di due sottospazi vettoriali di dimensione 3, la cui somma in
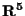
è un iperpiano vettoriale e la cui intersezione è un piano);
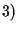
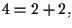
cioè
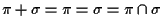
(è il caso dei proiettivizzati di due sottospazi vettoriali di
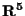
di dimensione 3 e uguali).
Nel caso
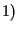
si dice che i piani
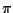
e
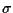
sono in posizione generale,
secondo la
definizione 31.




