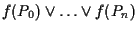10.1
Certamente
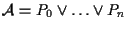 -abbiamo
-abbiamo 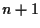 punti indipendenti in uno spazio affine di
dimensione
punti indipendenti in uno spazio affine di
dimensione 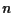 - per cui
- per cui
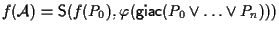 .
.
A questo punto, utilizzando prima parte di proposizione 9 e le considerazioni sulla giacitura di un sottospazio generato da punti, otteniamo
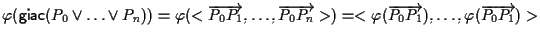 .
.
Ora basta applicare la definizione di applicazione affine per
ottenere
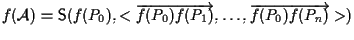 ,
ma grazie a quanto detto
sui sottospazi generati da punti (vedi nuovamente le considerazioni sulla giacitura di un sottospazio generato da punti) è immediato riconoscere che il
secondo membro è proprio
,
ma grazie a quanto detto
sui sottospazi generati da punti (vedi nuovamente le considerazioni sulla giacitura di un sottospazio generato da punti) è immediato riconoscere che il
secondo membro è proprio