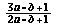Prova Scritta - Algebra e Geometria
14-01-2002 - A.A. 2002-2003 - Prof. A. Gimigliano
Siano r, s due rette in R3:
| r: |
 |
(a + 1)x + y = 2 |
s: |
|
(b + 1)x +2y + z = 2 |
| (2a + b + 2)x + 5y + kz = 7 |
(a + b + 2)x + 3y + z = 2 |
1) Determinare, al variare di k, se r ed s siano parallele, sghembe o incidenti.
2) Dare un valore a k tale che r e s siano sghembe. Determinare un punto P  r ed un punto Q s e determinare poi il piano perpendicolare alla retta per P e Q e passante per l'origine.
Assegnare ad a, b il valore delle ultime cifre del proprio numero di
matricola (ad esempio, se il numero è 1224567, allora a = 6, b =
7)
|
|
1) Ponendo r ed s a sistema si ottiene un sistema la cui matrice completa sarà:
| (A/B) = |
R1 |
 |
a+1 |
1 |
0 |
 |
-2 |
 |
(R4  R4- R3- R1) |
|
a+1 |
1 |
0 |
|
-2 |
|
R2 |
2a+b+2 |
5 |
k |
-7 |
2a+b+2 |
5 |
k |
-7 |
R3 |
b+1 |
2 |
1 |
-2 |
b+1 |
2 |
1 |
-2 |
R4 |
a+b+2 |
3 |
1 |
-2 |
0 |
0 |
0 |
2 |
|
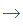(R2 R2- 2R1- R3) |
|
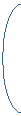a+1 |
1 |
0 |
|
-2 |
|
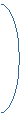-1 |
1 |
k-1 |
-1 |
b+1 |
2 |
1 |
-2 |
0 |
0 |
0 |
2 |
Possiamo notare che rg(A) < rg(A/B), quindi le rette non sono mai incidenti. Sviluppiamo il determinante del primo minore 3  3 ottenendo: k(2a - b + 1) - (3a - b + 1).
| Quindi per k ≠ |
 |
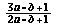, si ha che rg(A) = 3 e rg(A/B) = 4, cosicchè le rette sono SGHEMBE |
| Quindi per k = |
|
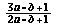, si ha che rg(A) = 2 e rg(A/B) = 3, cosicchè le rette sono PARALLELE. |
2) Poniamo ad esempio k=1. Scegliamo i punti P = (0, 2, -2) r, Q = (0, 1, 0) s; allora la retta per P e Q ha vettore direttore P - Q = (0, 1, -2). Per trovare allora il piano di equazione Ax + By + Cz + D = 0, perpendicolare alla retta PQ si potrà allora porre (A, B, C) = (0, 1, -2) e D = 0 (poichè deve passare per l'origine). Quindi il piano cercato ha equazione: y - 2z = 0 .
|
