Esempio

1.
Prendiamo in considerazione il prodotto scalare standard in $\mathbf{R}^{n}$, allora
$ \vert\vert\mathbf{v}\vert\vert=\vert\vert(v_{1},\ldots,v_{n})\vert\vert=\sqrt{ (v_{1},\ldots,v_{n})\cdot(v_{1},\ldots,v_{n})}=\sqrt{v_{1}^{2}+\cdots+v_{n}^{2}}$ e la distanza fra due vettori $\mathbf{u} \,$ e $\, \mathbf{v}$ si calcola come:

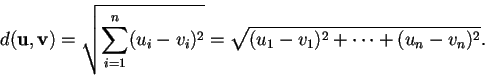
\begin{displaymath}d(\mathbf{u},\mathbf{v})= \sqrt {\sum_{i=1}^{n} (u_{i}-v_{i})^2}= \sqrt{(u_{1}-v_{1})^2+ \cdots +(u_{n}-v_{n})^2}. \end{displaymath}

2.
Sia $\mathbf{R}_{n}[x]$ lo spazio dei polinomi in una indeterminata a elementi reali; allora con la funzione prodotto scalare usata negli esempi del secondo capitolo, la norma risulta essere:

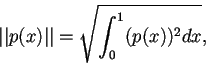
\begin{displaymath}\vert\vert p(x)\vert\vert= \sqrt{\int_{0}^{1} (p(x))^2 dx}, \end{displaymath}

mentre la distanza diventa:

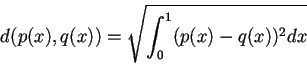
\begin{displaymath}d(p(x),q(x))= \sqrt{\int_{0}^{1} (p(x)-q(x))^2 dx} \end{displaymath}