Esempi

1.
Sia $K$ un campo, $n$ un intero positivo, allora la forma bilineare nulla su $K^{n} \times K^{n}$ è detta prodotto interno nullo.

2.
Sia $\mathbf{V}=\mathbf{R}^2$, allora la funzione
$q: \mathbf{R}^2 \rightarrow K$
$q(\mathbf{v})=q((x_{1},x_{2}))= x_{1}(x_{1}+x_{2})+x_{1}x_{2}$
è una forma quadratica.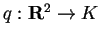

3.
Sia $n$ un intero positivo, indichiamo con $\mathbf{R}_{n}[x]$ lo spazio vettoriale dei polinomi in una indeterminata a coefficienti reali di grado $\leq n$. La funzione

\begin{displaymath}q: \mathbf{R}_{n}[x] \rightarrow K, \,\, \textrm{ con} \qquad q(p(x)):= \int_{0}^{1} (p(x))^{2}dx \end{displaymath}

dove $p(x)$ è un polinomio di $\mathbf{R}_{n}[x]$, è una forma bilineare quadratica .

4.
Supponiamo che sia $\mathbf{V}=\mathbf{R}^{3} $ e $\mathcal{E}$ la sua base canonica.
Consideriamo la matrice $A$:

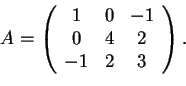
\begin{displaymath}A= \begin{array}({ccc}) 1 & 0 & -1\\ 0 & 4 & 2\\ -1 & 2 & 3 \end{array}. \end{displaymath}

Vogliamo calcolare sia la forma bilineare $f$ che la forma quadratica $q$ associate ad $A$.
Avremo:
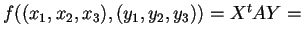
$f((x_{1},x_{2},x_{3}),(y_{1},y_{2},y_{3}))= X^{t}AY= $
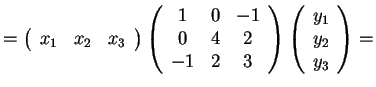
$=\begin{array}({ccc}) x_{1} & x_{2} & x_{3} \end{array} \begin{array}({ccc})... ... \end{array} \begin{array}({c}) y_{1} \\ y_{2} \\ y_{3} \end{array} = $

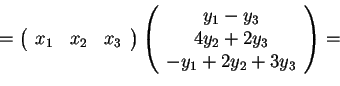
\begin{displaymath}=\begin{array}({ccc}) x_{1} & x_{2} & x_{3} \end{array} \b... ...3} \\ 4y_{2}+2y_{3} \\ -y_{1}+2y_{2}+3y_{3} \end{array}= \end{displaymath}

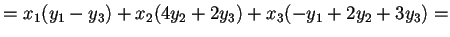
$=x_{1}(y_{1}-y_{3})+x_{2}(4y_{2}+2y_{3})+x_{3}(-y_{1}+2y_{2}+3y_{3})=$
$=x_{1}y_{1}-x_{1}y_{3}+4x_{2}y_{2}+2x_{2}y_{3}-x_{3}y_{1}+2x_{3}y_{2}+3x_{3}y_{3}$.
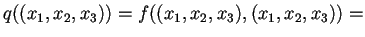
$q((x_{1},x_{2},x_{3}))= f((x_{1},x_{2},x_{3}),(x_{1},x_{2},x_{3}))=$ $=x_{1}^{2}+4x_{2}^{2}+3x_{3}^{2}-2x_{1}x_{3}+4x_{2}x_{3}$.