

- 1.
- Si consideri la forma bilineare
Dopo aver verificato che è una forma simmetrica, stabilire per quali valori di
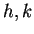 la seguente forma quadratica
è associata a
la seguente forma quadratica
è associata a 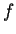 .
.
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
Soluzione
- I passo:
- La matrice associata a
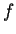 rispetto alla base canonica è:
rispetto alla base canonica è:
che è una matrice simmetrica; questo implica che 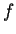 è simmetrica.
è simmetrica.
II passo:
Poiché la forma quadratica 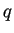 determina univocamente la forma bilineare simmetrica a cui è associata, anche la matrice relativa dovrà essere unica, quindi dovrà valere che:
determina univocamente la forma bilineare simmetrica a cui è associata, anche la matrice relativa dovrà essere unica, quindi dovrà valere che:
da cui si ottiene
Per queste due coppie di valori, le due forme sono equivalenti.





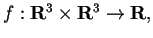
la seguente forma quadratica
è associata a.
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzionerispetto alla base canonica è:
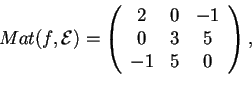
è simmetrica.
determina univocamente la forma bilineare simmetrica a cui è associata, anche la matrice relativa dovrà essere unica, quindi dovrà valere che:
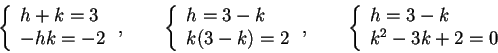
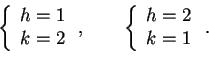



 Teoria
Teoria