

- 1.
- Date le equazioni cartesiane del sottospazio vettoriale
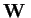 di
di
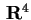 con il prodotto scalare standard,
con il prodotto scalare standard,
calcolare come si decompone
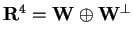 e la proiezione del vettore
e la proiezione del vettore
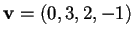 su
su
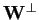 .
.
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
-
- Per calcolare la proiezione ortogonale di
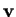 su
su
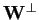 ,
prendiamo una base ortonormale del sottospazio partendo da quella fornita dai vettori che lo generano;
normalizziamo il primo vettore:
,
prendiamo una base ortonormale del sottospazio partendo da quella fornita dai vettori che lo generano;
normalizziamo il primo vettore:
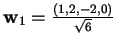 ;
;
e calcoliamo
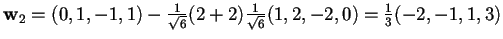 ;
;
che normalizzato diventa
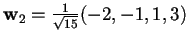 .
.
Quindi, considerata la base ortonormale
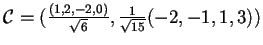 ,
applicando la formula (3), si ottiene la proiezione ortogonale:
,
applicando la formula (3), si ottiene la proiezione ortogonale:
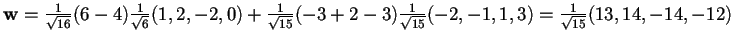 .
.





di
con il prodotto scalare standard,
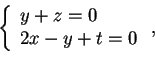
e la proiezione del vettore
su
.
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzione:
allora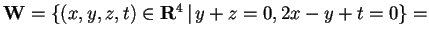
,
, e una base per
sarà
Per determinare.
, basta trovare le equazioni che risolvono il sistema omogeneo:
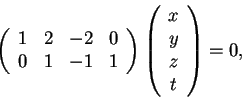
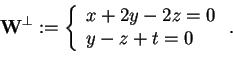
, perciò la decomposizione di
sarà
infatti i quattro vettori sono fra loro linearmente indipendenti, quindi generano tutto,
e in più ne formano anche una base.

su
, prendiamo una base ortonormale del sottospazio partendo da quella fornita dai vettori che lo generano; normalizziamo il primo vettore:
;
;
.
, applicando la formula (3), si ottiene la proiezione ortogonale:
.



 Teoria
Teoria