

- 1.
- Consideriamo il prodotto scalare standard su
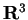 e il sottospazio
e il sottospazio
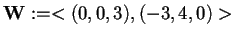 .
Per determinare la proiezione ortogonale del vettore
.
Per determinare la proiezione ortogonale del vettore
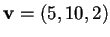 su
su
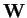 ,
prendiamo una base ortonormale di
,
prendiamo una base ortonormale di
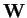 :
per procedere in modo semplice e efficace, possiamo prendere la base formata dai vettori linearmente indipendenti che generano il sottospazio ,
:
per procedere in modo semplice e efficace, possiamo prendere la base formata dai vettori linearmente indipendenti che generano il sottospazio ,
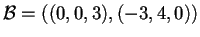 ,
e, poiché è già ortogonale, normalizzarla; quindi otteniamo
,
e, poiché è già ortogonale, normalizzarla; quindi otteniamo
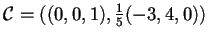 .
.
Applicando la formula (3), abbiamo che la proiezione ortogonale risulta essere:
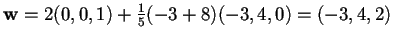
,
mentre la perpendicolare a
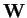 sarà:
sarà:
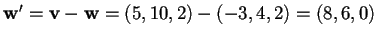
.
- 2.
- Dato su
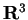 il prodotto scalare standard, vogliamo calcolare l'angolo
il prodotto scalare standard, vogliamo calcolare l'angolo 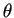 fra i vettori
fra i vettori
Allora si ha che:




e il sottospazio
. Per determinare la proiezione ortogonale del vettore
su
, prendiamo una base ortonormale di
: per procedere in modo semplice e efficace, possiamo prendere la base formata dai vettori linearmente indipendenti che generano il sottospazio ,
, e, poiché è già ortogonale, normalizzarla; quindi otteniamo
.
,
sarà:
.
il prodotto scalare standard, vogliamo calcolare l'angolo
fra i vettori
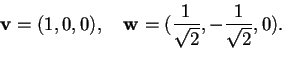
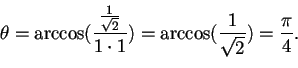


 Teoria
Teoria