
Esercizi

- 1.
- Si consideri
Si determini un vettore
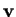 non nullo e isotropo tale che
non nullo e isotropo tale che
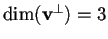 ,
un vettore
,
un vettore
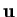 non isotropo tale che
non isotropo tale che
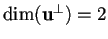 ,
e si provi che il vettore
,
e si provi che il vettore
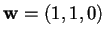 è isotropo e tale che
è isotropo e tale che
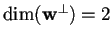 .
.
È possibile trovare un vettore
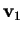 non isotropo e tale che
non isotropo e tale che
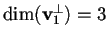 ?
?
Vuoi un aiuto?
Per vedere la soluzione totale, clicca  ,
oppure clicca
,
oppure clicca  per visualizzare ogni singolo passo della soluzione.
per visualizzare ogni singolo passo della soluzione.
Infine, la quarta richiesta è impossibile da soddisfare, perché
se
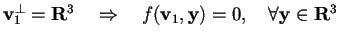 ,
,
ma questo implicherebbe che
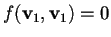 perché
perché
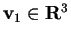 ,
quindi
,
quindi
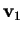 dovrebbe essere un vettore isotropo; e questo contraddice le ipotesi.
dovrebbe essere un vettore isotropo; e questo contraddice le ipotesi.





non nullo e isotropo tale che
, un vettore
non isotropo tale che
, e si provi che il vettore
è isotropo e tale che
.
non isotropo e tale che
?
, oppure clicca
per visualizzare ogni singolo passo della soluzione.
Soluzione.
, infatti
. Inoltre
, perché
; in dettaglio:
(perché
);
.
.
, allora
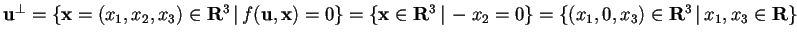
che è un sottospazio di dimensione 2 perché generato da due vettori linearmente indipendenti.
.
,
perché
, quindi
dovrebbe essere un vettore isotropo; e questo contraddice le ipotesi.



 Teoria
Teoria