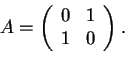Complementi

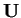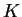Sia $\mathbf{U}$ un $K$-spazio vettoriale di dimensione 2.
Supponiamo sia assegnata una forma bilineare simmetrica 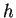$h$ non degenere tale che esista un vettore isotropo rispetto ad 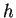$h$ e non nullo. Allora 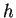$h$ si dice forma iperbolica su 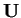$\mathbf{U}$ e la coppia 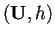$(\mathbf{U},h)$ si dice piano iperbolico.
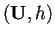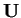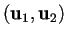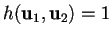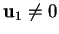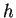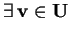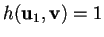Se $(\mathbf{U},h)$ è un piano iperbolico, $\mathbf{U}$ possiede una base $(\mathbf{u}_{1},\mathbf{u}_{2})$ formata da due vettori isotropi tali che $h(\mathbf{u}_{1},\mathbf{u}_{2})=1$. Infatti per definizione esiste $\mathbf{u}_{1} \neq 0$ isotropo ; poiché $h$ è non degenere, $\exists \, \mathbf{v} \in \mathbf{U}$ tale che $h(\mathbf{u}_{1},\mathbf{v})=1$.
I vettori 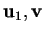$\mathbf{u}_{1}, \mathbf{v}$ sono linearmente indipendenti, pertanto costruendo il vettore
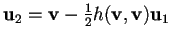
$\mathbf{u}_{2}=\mathbf{v}-\frac{1}{2}h(\mathbf{v},\mathbf{v})\mathbf{u}_{1}$,
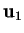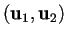si ottiene un vettore non proporzionale a $\mathbf{u}_{1}$, quindi la base $(\mathbf{u}_{1},\mathbf{u}_{2})$ è quella richiesta, detta iperbolica.
La matrice associata di 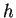$h$ rispetto ad una base iperbolica è quindi

\begin{displaymath}A=\begin{array}({cc}) 0 & 1\\ 1 & 0 \end{array}. \end{displaymath}

Viceversa, se in uno spazio vettoriale 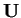$\mathbf{U}$ una forma bilineare 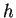$h$ ha matrice associata uguale ad 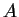$A$, allora la base relativa è iperbolica e 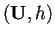$(\mathbf{U},h)$ è un piano iperbolico.