pro5

Osservazione 1

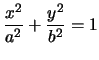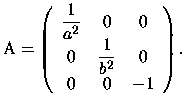Consideriamo la seguente ellisse scritta in coordinate affini: $\displaystyle\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ . Essa ha come matrice $\mathrm A=\left( \begin{array}{ccc} \displaystyle\frac{1}{a^2} & 0 & 0\\ 0 & \displaystyle\frac{1}{b^2} & 0\\ 0 & 0 & -1 \end{array} \right).$ In coordinate proiettive l'equazione diventa 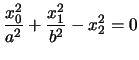$\displaystyle\frac{x_0^2}{a^2}+\frac{x_1^2}{b^2}-x_2^2=0$ . 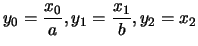Nelle coordinate $y_0=\displaystyle\frac{x_0}{a}, y_1=\displaystyle\frac{x_1}{b}, y_2=x_2$ l'equazione è

$\begin{displaymath} y_0^2+y_1^2-y_2^2=0. \end{displaymath}$

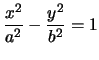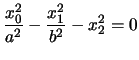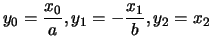Se consideriamo l'iperbole $\displaystyle\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ in coordinate proiettive sarà $\displaystyle\frac{x_0^2}{a^2}-\frac{x_1^2}{b^2}-x_2^2=0$ . Nelle coordinate $y_0=\displaystyle\frac{x_0}{a}, y_1=-\displaystyle\frac{x_1}{b}, y_2=x_2$ l'equazione è

$\begin{displaymath} y_0^2+y_1^2-y_2^2=0. \end{displaymath}$

Se consideriamo infine la parabola 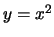. La sua matrice è 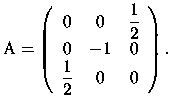$\mathrm A=\left( \begin{array}{ccc} 0 & 0 &\displaystyle\frac{1}{2} \\ 0 & -1 & 0\\ \displaystyle\frac{1}{2} & 0 & 0 \end{array} \right).$ La conica proiettiva è 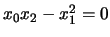. La segnatura è 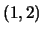, cambiando di segno abbiamo 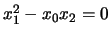con segnatura 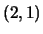. Si vede subito che tale equazione rappresenta una forma quadratica che è possibile diagonalizzare. In coordinate opportune, quindi 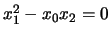diventa

$\begin{displaymath} y_0^2+y_1^2-y_2^2=0. \end{displaymath}$

Riassumendo possiamo dire che ellisse, parabola, iperbole sono coniche affini corrispondenti alla stessa conica proiettiva, quella che abbiamo chiamato conica generale. Allo stesso modo si dimostra che due rette affini incidenti o rette parallele corrispondono sempre alla stessa conica proiettiva .