Osservazione 2
Nel piano 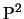 intersechiamo una conica
intersechiamo una conica 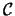 con
la retta impropria (o retta all'infinito) di
equazione
con
la retta impropria (o retta all'infinito) di
equazione 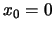 .
.
-
Consideriamo un'ellisse E di equazione
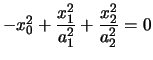 .
.
Quindi non vi sono intersezioni con la retta all'infinito.
-
Consideriamo un'iperbole I di equazione
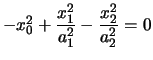 .
.
I punti di intersezione con la retta all'infinito sono quindi:
In quanto
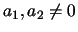
abbiamo che i due punti trovati non
coincidono. Allora la retta impropria interseca un'iperbole in due
punti distinti che sono i punti all'infinito delle rette
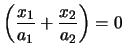
,
e
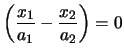
, cioč dei suoi due
asintoti.
-
Consideriamo una parabola P di equazione
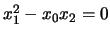 .
.
quindi le due soluzioni sono
coincidenti. La parabola č tangente alla retta all'infinito
nel punto
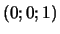
.
Figura:
Nel passaggio dal piano ordinario
a quello ampliato con i punti impropri l'iperbole č stata
completata con l'aggiunta di due punti, la parabola con l'aggiunta
di un solo punto. In ogni caso esse appaiono come curve
chiuse al pari dell'ellisse.
|
|
![]() intersechiamo una conica
intersechiamo una conica ![]() con
la retta impropria (o retta all'infinito) di
equazione
con
la retta impropria (o retta all'infinito) di
equazione ![]() .
.
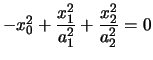 .
.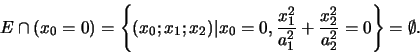
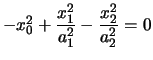 .
.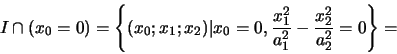
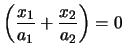 ,
e
,
e
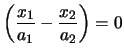 , cioč dei suoi due asintoti.
, cioč dei suoi due asintoti.
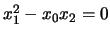 .
.![\includegraphics[width=9cm,height=9cm]{coniche_proiettive.ps}](img17.png)