Diamo ora un teorema di classificazione delle coniche in 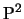$\mathrm P^2$.

Teorema 1 
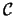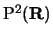Ogni conica $\mathcal C$ di $\mathrm P^2(\mathbf R)$ è proiettivamente equivalente a una delle seguenti:

\begin{displaymath} \begin{array}{ll} x_0^2+x_1^2-x_2^2=0 \qquad & \qquad \tex... ...& \qquad \textit{conica doppiamente degenere}\\ \end{array} \end{displaymath}

Queste cinque coniche sono a due a due non proiettivamente equivalenti. Tali equazioni vengono chiamate FORME CANONICHE.

 

Dimostrazione

Definizioni Osservazione 1