Classificazione delle coniche proiettive
Sia
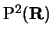 il piano proiettivo su
il piano proiettivo su 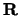 .
.
Ricordiamo che i punti e le rette di 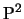 sono gli
stessi di quelli di
sono gli
stessi di quelli di
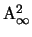 , dove
, dove
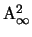 rappresenta
rappresenta 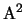 completato con l'aggiunta
della retta impropria (completamento proiettivo del piano
affine).
L'equazione di una conica
completato con l'aggiunta
della retta impropria (completamento proiettivo del piano
affine).
L'equazione di una conica 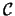 del piano
del piano 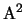 in
coordinate omogenee si può quindi scrivere nel modo
seguente:
in
coordinate omogenee si può quindi scrivere nel modo
seguente:
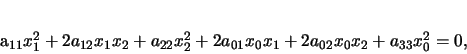 |
(1) |
con gli
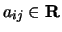 non tutti nulli.
La conica scritta in coordinate omogenee come in
(
non tutti nulli.
La conica scritta in coordinate omogenee come in
(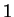 ) rappresenta una conica in
) rappresenta una conica in 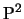 .
La matrice
.
La matrice
è una matrice simmetrica ottenuta ponendo 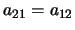 ,
,
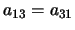 ,
, 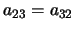 . Tale matrice ci permette di
rappresentare la conica (
. Tale matrice ci permette di
rappresentare la conica (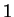 ) mediante l'equazione
) mediante l'equazione
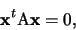 |
(2) |
dove x=
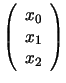 è il vettore delle indeterminate.
Sia ora
è il vettore delle indeterminate.
Sia ora 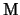 una matrice
una matrice 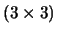 a coefficienti in
a coefficienti in
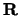 , invertibile. Se prendiamo il vettore
, invertibile. Se prendiamo il vettore
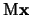 e lo sostituiamo ad x nella
(
e lo sostituiamo ad x nella
(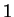 ), oppure nella (
), oppure nella (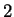 ) otteniamo una nuova
equazione e cioè:
) otteniamo una nuova
equazione e cioè:
da cui
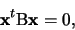 |
(3) |
dove
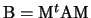 .
.
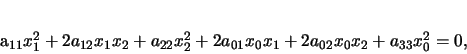

![]() ,
,
![]() ,
, ![]() . Tale matrice ci permette di
rappresentare la conica (
. Tale matrice ci permette di
rappresentare la conica (![]() ) mediante l'equazione
) mediante l'equazione
 è il vettore delle indeterminate.
Sia ora
è il vettore delle indeterminate.
Sia ora