Si consideri il campo
K (ad esempio
K = R , C ).
Ad ogni matrice quadrata
A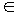 
M n,n(K)
si associa un valore di K,
detto determinante di A,
rappresentato dal simbolo
il determinante è dunque una applicazione
|
 |
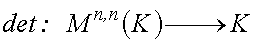
Lo scopo dell'introduzione del determinante è fondamentalmente quello di avere una
funzione che "controlla" il rango della matrice:
vedremo che
 |
|
Per valori di n piccoli (n = 1,2,3)
il determinante di una matrice lo si può calcolare con semplicità, mentre in generale
la sua definizione (regola di Laplace) è piuttosto complessa.
Per n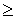 4
non esistono espressioni rapide (come per n=1,2) né scorciatoie (n=3) per il
calcolo del determinante e quindi ci si rifà alla regola di Laplace
|
|
