Esempi
di successioni reali
1) 
,
ove 
(si parla di
successione
costante).
2) 
.
Si
tratta
di un esempio in cui i valori che assumono i termini della successione
costituiscono
un insieme finito:
in
questo
caso, i valori sono esattamente due, cioè 1 e – 1
(alternativamente).
3) 
,
ove 
.
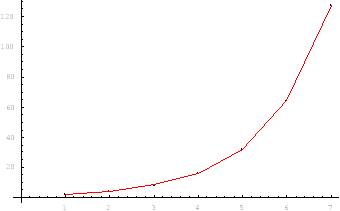
an =
2n
4) 
,
ove .
5) 
.
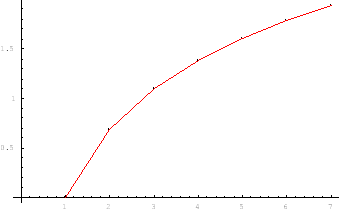
an =
log n
6) Successioni
definite per ricorrenza
(o ricorsive).
Si tratta di successioni del tipo seguente:
, 
con 
funzione reale.
Un esempio di successione ricorsiva è
dovuta ad Erone
e permette di calcolare approssimativamente la radice di un numero
reale x:
La definizione di successione ricorsiva si
può
estendere al caso in cui sono coinvolti più di un termine; ci
limitiamo ad
enunciare il caso di due termini:
,
. 
con 
funzione di due
variabili reali.
Un esempio di successione
ricorsiva è la successione
di Fibonacci (vedi Introduzione).
