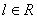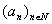
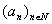
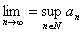
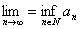TEOREMA (5.2)  Sia    una successione di numeri reali.

 1)        Se (a_n)  è una successione monotona crescente, allora    .

 2)     Se (a_n) è una successione monotona decrescente, allora   .

Dimostrazione

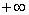
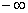
    Dobbiamo anzitutto osservare che la dimostrazione richiede di provare, sia per il punto 1) che per il punto 2), sia i casi in cui estremo superiore e inferiore sono numeri reali che i casi in cui sono  o  .

    Dimostriamo solo la parte 1) del teorema: la parte 2) è del tutto analoga alla prima con i segni di uguaglianza “invertiti”.

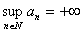
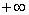
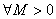
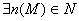
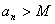
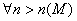
-         Primo caso:  . Ricordando la definizione di divergenza a :

,  : , 

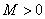
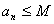
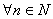
    Se per assurdo, dunque, la successione non divergesse positivamente, esisterebbe  tale che , . La successione sarebbe, così, superiormente limitata e ciò sarebbe assurdo, in quanto contro l’ipotesi.

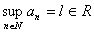
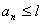
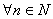
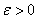
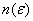
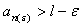
-         Secondo caso:  . E’ evidente che dall’ipotesi segue che  ,  e che, per ogni fissato , esiste un indice  tale che :

                                .

    Perciò, si ottiene che, per la monotonia di  :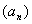

, 

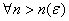
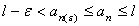
    In definitiva, si ha:

,  :   , 

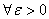
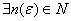
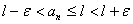
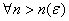
che per definizione ci dà la convergenza della successione a   .

Back