Logica predicativa del 1° ordine
La logica predicativa del 1° ordine è forse
la logica più nota al grande pubblico
dei matematici.
Sostanzialmente, si tratta di un'estensione della logica proposizionale con i
quantificatori per ogni (indicato con 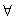 ) e esiste
(indicato con
) e esiste
(indicato con 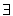 ), variabili, costanti e predicati.
Alcune formulazioni contengono anche funzioni, ma poichè
queste possono essere rappresentate da predicati si tratta più
di una scelta notazionale che di una differenza nelle capacità
della logica.
), variabili, costanti e predicati.
Alcune formulazioni contengono anche funzioni, ma poichè
queste possono essere rappresentate da predicati si tratta più
di una scelta notazionale che di una differenza nelle capacità
della logica.
Per esempio, l'affermazione "Ogni uomo che ha un cane lo porta a
spasso" si traduce così:
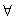 x ((UOMO(x)
x ((UOMO(x) 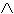
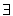 y
(CANE(y)
y
(CANE(y) 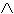 HA(x,
y)))
HA(x,
y))) 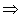 PORTA_A_SPASSO(x, y))
PORTA_A_SPASSO(x, y))
Questa logica si dice di primo ordine
perchè in essa le variabili possono rappresentare oggetti, ma
non predicati. Questa limitazione ha conseguenze piuttosto gravi sulla
capacità espressiva della logica del primo ordine, in quanto non
è
possibile ad esempio giustificare nella logica del primo ordine un
ragionamento del tipo
Il cancello è rosso;
Il rosso è un colore;
Quindi, il cancello ha un colore.
Inoltre, in questa logica è
impossibile esprimere il principio di induzione matematica, e di
conseguenza i numeri naturali (definiti attraverso gli assiomi di
Peano) non sono definibili.
Esistono
logiche di ordine superiore che non hanno queste restrizioni:
però, come ha dimostrato
Göodel, per queste logiche (e, in generale, per ogni logica
"abbastanza potente" da poter rappresentare i numeri naturali) non
esiste nessun algoritmo che, data una proposizione qualsiasi del
linguaggio, ne calcoli in tempo finito il valore di verità.
Testi
consigliati: Qualunque libro di logica elementare
conterrà certamente
un'ampia sezione su questa importantissima logica. Alcuni testi (tutti
presenti nella biblioteca
del Dipartimento di Matematica di Bologna) che ci sentiamo di
consigliare sono:
- Asperti, Ciabattoni: "Logica a Informatica";
- Bell, Machover: "A course in Matematical Logic";
- Gamut, L.T.F.: "Logic, Language and Meaning"
(primo volume).
Di questi, il
primo è il più interessato agli aspetti algoritmici del
problema di ricerca delle tautologie; il secondo, forse il più
"matematico"
dei tre, copre (in maniera abbastanza formale) buona parte degli
argomenti principali della logica matematica; il terzo, infine,
presenta la logica proposizionale e la logica predicativa
(così come altre logiche meno conosciute) da un punto di vista
più discorsivo, ed è particolarmente interessato al
problema dell'analisi del linguaggio naturale attraverso strumenti di
logica matematica.
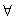 ) e esiste
(indicato con
) e esiste
(indicato con 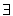 ), variabili, costanti e predicati.
Alcune formulazioni contengono anche funzioni, ma poichè
queste possono essere rappresentate da predicati si tratta più
di una scelta notazionale che di una differenza nelle capacità
della logica.
), variabili, costanti e predicati.
Alcune formulazioni contengono anche funzioni, ma poichè
queste possono essere rappresentate da predicati si tratta più
di una scelta notazionale che di una differenza nelle capacità
della logica.
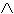
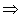 PORTA_A_SPASSO(
PORTA_A_SPASSO(