La logica proposizionale
In queste pagine
definiremo formalmente la logica proposizionale. Si noti come, grazie
alle definizioni precedenti, è
possibile caratterizzare facilmente la logica proposizionale.
Le formule
ben formate della logica proposizionale sono quelle generate
dalla seguente grammatica context-free:
-
Simboli non
terminali: P (proposizione).
-
Simboli terminali: Un
numero arbitrariamente grande di proposizioni elementari
A,..,Z,... , i connettivi
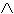 (E),
(E), 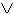 (OPPURE),
(OPPURE), 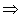 (IMPLICA), ¬ (NON) e le parentesi ( e );
(IMPLICA), ¬ (NON) e le parentesi ( e );
-
-
Le seguenti regole di
produzione: P → (P 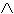 P), P → (P
P), P → (P 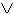 P), P → (P
P), P → (P 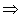 P), P → (¬P);
P), P → (¬P);
-
Il simbolo iniziale è naturalmente P.
I valori di
verità
della logica proposizionale sono 1 (vero) e 0 (falso): si tratta
dunque di una logica bivalente.
Un modello M per
la
logica proposizionale è dato dal valore di verità Å
assegnato ad ogni proposizione elementare A.
La funzione di verità
V per la logica proposizionale è così definita:
-
V(A, M) = Å
per ogni proposizione elementare A;
-
V (α 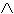 β) = il minimo tra V (α) e V
(β);
β) = il minimo tra V (α) e V
(β);
-
V (α 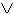 β) = il massimo tra V (α) e V
(β);
β) = il massimo tra V (α) e V
(β);
-
V (¬ α) = 1 - V (α);
-
V (α 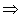 β) = V ((¬ α)
β) = V ((¬ α) 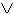 β);
β);
In questo modo abbiamo
definito in maniera soddisfacente l'intera logica proposizionale.
Semplice, vero?
Comunque, è
opportuno fare alcune considerazioni sui
connettivi.
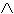 (E),
(E), 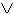 (OPPURE),
(OPPURE), 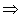 (IMPLICA), ¬ (NON) e le parentesi ( e );
(IMPLICA), ¬ (NON) e le parentesi ( e ); 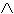 P), P → (P
P), P → (P 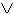 P), P → (P
P), P → (P 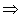 P), P → (¬P);
P), P → (¬P);