Considerazioni sui connettivi
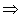
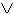
·
Valgono inoltre le leggi di De Morgan:
V(α 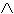 β) = V(¬(¬(α)
β) = V(¬(¬(α) 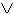 ¬(β))) e V(α
¬(β))) e V(α 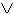 β) = V(¬(¬(α)
β) = V(¬(¬(α) 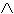 ¬(β))).
¬(β))).
La
dimostrazione, al solito, è lasciata al lettore.
· È
anche possibile definire 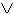 e
e 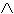 a partire da ¬ e
a partire da ¬ e 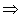 ; infatti
(anche qui la verifica è lasciata al lettore):
; infatti
(anche qui la verifica è lasciata al lettore):
V(α 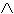 β) = V(¬(α
β) = V(¬(α 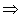 ¬(β)))
e V(α
¬(β)))
e V(α 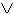 β) = V(¬(α)
β) = V(¬(α) 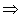 β)
β)
Quindi
sarebbe possibile definire solo ¬ e uno qualunque tra 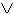 ,
, 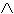 e
e 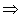 , e poi trattare tutti gli altri
connettivi come semplici abbreviazioni.
, e poi trattare tutti gli altri
connettivi come semplici abbreviazioni.
Può
sorprendere scoprire che in effetti esistono due connettivi a due
posti ognuno dei quali basta per definire qualsiasi altro connettivo!
Il primo
di questi, che chiameremo NOR (NOT OR), equivale alla
costruzione verbale "nè α nè β”, e il
suo valore di verità è definito come
segue:
V(α
NOR β) = 1 - il massimo
tra V(α) e V(β),
ovvero
V(α NOR β) = V(¬(α 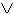 β)).
β)).
Per
dimostrare che gli altri connettivi sono definibili in termini di
questo ci basta costruire ¬ e 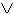 , che abbiamo
visto essere sufficienti per
definire tutti gli altri connettivi. Questo è facile, e al
solito le verifiche
vengono lasciate al lettore:
, che abbiamo
visto essere sufficienti per
definire tutti gli altri connettivi. Questo è facile, e al
solito le verifiche
vengono lasciate al lettore:
· V(¬(α)) =
1 - V(α) = V(α NOR α)
· V(α 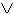 β) = V(¬(α NOR β)) = V((α NOR
β) NOR (α
NOR β)
β) = V(¬(α NOR β)) = V((α NOR
β) NOR (α
NOR β)
Il
secondo, che chiameremo NAND (NOT AND), non ha un equivalente nel
linguaggio umano. La maniera più conveniente per descriverne il
significato è
un'espressione del tipo " una delle seguenti affermazioni è
falsa". È
definito come segue:
V(α
NAND β) = 1 - il minimo
tra V(α) e V(β),
ovvero
V(α NAND β) = V(NOT(α 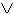 β)).
β)).
Per
dimostrare che gli altri connettivi sono definibili in termini di
questo ci basta costruire il NOT e l'AND, che abbiamo visto essere
sufficienti
per definire tutti gli altri connettivi. Come al solito le verifiche
vengono
lasciate al lettore:
· V(¬(α))
= 1 - V(α) = V(α NAND α)
· V(α
∧ β) = V(¬(α NAND
β))
= V((α NAND β) NAND (α NAND β)
Un'osservazione
ulteriore sull'implicazione: la definizione data non
cattura interamente il significato intuitivo dell'implicazione. "A 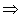 B" è una tautologia se e solo
se non è possibile che A sia
vero mentre B è falso, il che corrisponde alla nostra
intuizione;
tuttavia, ((A
B" è una tautologia se e solo
se non è possibile che A sia
vero mentre B è falso, il che corrisponde alla nostra
intuizione;
tuttavia, ((A 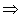 B)
B) 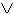 (B
(B 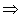 A)) è sempre una
tautologia (la facile verifica è lasciata al lettore), il che
è estremamente
controintuitivo!
A)) è sempre una
tautologia (la facile verifica è lasciata al lettore), il che
è estremamente
controintuitivo!
Per una definizione soddisfacente dell'implicazione è giocoforza passare alle logiche modali