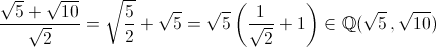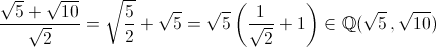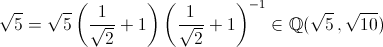Soluzione
11.
Si
ha che Q(√5+√10)⊆Q(√5,√10)
in quanto √5+√10∈Q(√5,√10).
Infatti Q(√5,√10)
è un campo, quindi la somma di due
suoi elementi gli appartiene.
Inoltre
Q(√5,√10)⊆Q(√5+√10)
in quanto √5∈Q(√5+√10)
e √10∈Q(√5+√10).
Infatti:
- √5∈Q(√5+√10):
√2∈Q(√5+√10)
(vedi esercizio 10)
dunque, essendo Q(√5+√10)
un campo, contiene la somma e il prodotto di due suoi elementi
qualsiasi, l'opposto
di ogni elemento e l'inverso
di ogni elemento non nullo. Quindi:
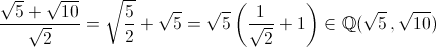
Quindi:
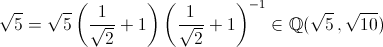
- √10∈Q(√5+√10):
√5∈Q(√5+√10)
e √2∈Q(√5+√10)
implicano che anche il prodotto √10=√5·√2
appartiene al campo.
Torna
agli esercizi.
Torna
alla teoria.
Vai
all'esercizio 12.