EQUAZIONI DIFFERENZIALI LINEARI DI ORDINE N

Una volta garantiti i risultati di esistenza ed unicità della soluzione, le equazioni differenziali lineari di ordine N vengono trattate in modo “autonomo” per quello che riguarda la ricerca delle soluzioni.

Per equazione differenziale lineare di ordine N a coefficienti continui, intendiamo:

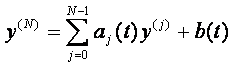
dove a_j( t ) e b( t ), i coefficienti, sono funzioni continue.

Importante per la trattazione generale è la considerazione dell’equazione

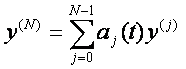
detta equazione omogenea associata.

Indichiamo con K l’insieme delle soluzioni dell’equazione omogenea: si può dimostrare che K è uno spazio vettoriale di dimensione N.

DEFINIZIONE: Una base {u₁,…,u_N} di K si chiama sistema fondamentale di integrali dell’equazione omogenea.