Torna all'indice Esempi

  1. Sia A Î Mm,n(K), una matrice di ordine m ´ n su di un campo K.
    La matrice A determina l’applicazione T : Kn ® Km definita da vAv in cui i vettori in Kn e Km sono scritti come vettori colonna. T è lineare.
    Infatti, per le proprietà delle matrici, " v, w Î Kn e k Î K si ha :

    T (v + w) = A (v + w) = Av + Aw = T (v) + T (w) e T (kv) = A (kv) = k Av = kT (v).

     

    Nota

  2. Sia V uno spazio vettoriale sul campo K e siano U, W due sottospazi supplementari in V, cioè sia

    V = U Å W.

    Poichè ogni v Î V si esprime in modo unico come v = u + w, u Î U, w Î W, possiamo definire l’applicazione

    p : V ® W ponendo p (u + w) = w.

    p è la proiezione di V su W definita dalla decomposizione V = U Å W. p è un’applicazione lineare.

    Infatti, se v1 = u1 + w1, v2 = u2 + w2 Î V, c1, c2 Î K, allora:

    p (c1v1 + c2v2) = p (c1u1 + c1w1 + c2u2 + c2w2) = p (c1u1 + c2u2 + c1w1 + c2w2) = c1w1 + c2w2 =

    = c1p (v1) + c2p (v2).


    Se in particolare W è un iperpiano, allora U = á u ñ per qualche u Î V \ W, e in questo caso p è detta proiezione di V su W nella direzione á u ñ .
    Se p è il piano ordinario, r una sua retta , V e W sono gli R-spazi vettoriali dei vettori geometrici di p e di r rispettivamente, e u Î V\W è un vettore non parallelo a r, la proiezione di V su W nella direzione
    á uñ è l'applicazione illustrata nella figura 1.1 .

    figura 1.1

    In modo simile, fissato un piano p nello spazio ordinario S , detti V e W gli spazi dei vettori geometrici di S e di p rispettivamente, e fissato u Î V\W, si descrive la proiezione p di V su W nella direzione á u ñ
    (fig. 1.2).

    figura 1.2

     

     

  3. Per ogni V e W, K-spazi vettoriali, l’applicazione nulla 0 : V ® W, definita da

    0 (v) = 0 Î W

    " v Î V, è un’applicazione lineare. Infatti " v,w Î V e " k Î K, si ha :

    0 (v + w) = 0 = 0 + 0 = 0 (v) + 0 (w) e 0 (kv) = 0 = k 0 = k 0 (v).

     

     


  4. In ogni spazio vettoriale V l’applicazione identica I : V ® V che manda ogni v Î V in sé stesso è lineare.
    Infatti " v, w Î V e " k, h Î K,

    I (kv + hw) = kv + hw = k I (v) + h I (w).

  5. Sia V lo spazio vettoriale di polinomi nella variabile t sul campo reale R.

    Sono lineari :


    Infatti " u, v Î V e k Î R,

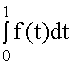    		e

    che è come dire D (u + v) = D (u) + D (v) e D (ku) = kD (u) ;

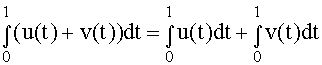    e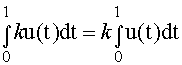

    cioè I (u + v) = I (u) + I (v) e I (ku) = k I (u).

     

     
  6. Siano V e U due K- spazi vettoriali. Sia F : V ® U un’applicazione lineare iniettiva e suriettiva.
    L’applicazione inversa F -1 : U ® V è lineare.
    Sia u1, u2 Î U. Poiché F è iniettiva e suriettiva, esistono dei vettori unici v1, v2 Î V per i quali
    F (v1) = u1e F (v2) = u2.
    Siccome F è lineare si ha :

    F (v1 + v2) = F (v1) + F (v2) = u1 + u2 e F (kv1) = kF (v1) = ku1.

    Per definizione di applicazione inversa,
    F -1 (u1) = v1, F -1 (u2) = v2, F -1 (u1 + u2) = v1 + v2 e F -1 (ku1) = kv1. Allora :

    F -1 (u1 + u2) = v1 + v2 = F -1 (u1) + F -1 (u2) e F -1(ku1) = kv1 = kF -1 (u1) .

     

     


  7. Siano V, W, Z dei K-spazi vettoriali.
    Siano F: V ® W ed G : W ® Z due applicazioni lineari. Allora la composizione G F : V ® Z è un’applicazione lineare.

    Si ha, per definizione di composizione di applicazioni, (GF)(v) = G(F(v)) per ogni v Î V ;

    pertanto per ogni v, u Î V :

    (GF)(u + v) = G(F(u + v)) = G(F(u) + F(v)) = G(F(u)) + G(F(v)) = (GF)(u) + (GF)(v).

    Inoltre per ogni kÎK si ha :

    (GF)(kv) = G(F(kv)) = G(kF(v)) = kG(F(v)) = k(GF)(v).
    argomento successivo