

 Prova d'esame del 28-02-1995
Prova d'esame del 28-02-1995
At = 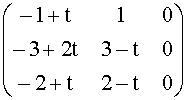
dove t è un parametro complesso.
A =  .
.
e = (1, x - 2, (x - 2)2), f = (1, x + 1, (x + 1)2).
 Prova d'esame del 6-06-1995
Prova d'esame del 6-06-1995
At = 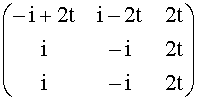 .
.
e = (e11, e12, e21, e22),
dove eij è la matrice con 1 al posto (i, j) e 0 altrove. Sia
A = 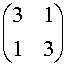 Î
M2(R),
Î
M2(R),
e consideriamo l'operatore lineare ![]() : M2(R) ®
M2(R) definito da
: M2(R) ®
M2(R) definito da ![]() (X) = AX.
(X) = AX.
 Prova d'esame del 11-09-1995
Prova d'esame del 11-09-1995
At = .
.
T(x, y, z) = (x - 3y + z, x - 3y + z, x - 3y + z).
Esiste una base v di R3 tale che Mv(T) = At per qualche valore di t?
 Prova d'esame del 9-10-1995
Prova d'esame del 9-10-1995
Sia
Ah = 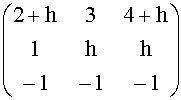
dove h è un parametro reale.
 |