Corso di Laurea in Matematica

 Prova d'esame del 8/06/1996
Prova d'esame del 8/06/1996
Nello spazio vettoriale R4 si considerino i vettori:
v1 = (1, 0, 1, -1), v2 = (0, 0, 2, 1), v3 = (2, 1, 2, -1), v4 = (0, 0, 0, 3), e i sottospazi:
Z = áv3 + v4ñ
, U = á
v1, v2ñ, W = áv3, v4ñ.
- Si dica se le somme Z + U e Z + U + W sono somme dirette, e si provi che U e W sono supplementari in R4.
- Sia pU: R4®
U la proiezione su U associata alla decomposizione
R4 = U Å
W; si determini MB,E(pU), dove B è la base (v1, v2), ed E è la base canonica di R4.
- Esiste un endomorfismo F di R4 tale che Ker(F) =U e dim Im(F 2) = 1?
- Si costruisca un endomorfismo G di R4 tale che G non sia l'identità, G(U) Í U, G(W) Í W, e G sia diagonalizzabile.
- Si costruisca un endomorfismo G di R4 tale che G(U)Í U, G(W) Í
W, e G non sia diagonalizzabile.
 Prova d'esame del 10/07/1996
Prova d'esame del 10/07/1996
In V = M2(R) si considerino i sottospazi:
U = á
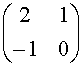 ñ
, W = {
ñ
, W = {
 , a, b Î
R },
T = á
, a, b Î
R },
T = á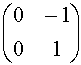 ,
, 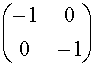 ñ.
ñ.
- Si dica se le somme U + W, e U + W + T sono somme dirette oppure no.
- Si costruisca FÎ
End(V) tale che Ker(F) = W e F/U= id U.
- Può una F come in b) essere diagonalizzabile? E non diagonalizzabile? In entrambi i casi, in caso di risposta positiva se ne costruisca una.
 Prova d'esame del 23/09/1996
Prova d'esame del 23/09/1996
- Nello spazio vettoriale V:= M2(R) si consideri il sottospazio
U:= á
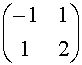 ,
, 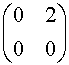 ñ
.
ñ
.
- Si costruisca un'applicazione F: R3®
V lineare, non iniettiva, e tale che UÍ
Im F.
- E' possibile trovare due basi B, C rispettivamente per R3 e per V tali che MC,B(F) non abbia alcuna colonna nulla?
- Esiste G: V®
V non identicamente nulla, e tale che G
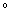 F sia l'applicazione nulla?
F sia l'applicazione nulla?
- Si determinino due sottospazi non nulli W, T di V tali che la somma
> U + W + T sia diretta. E' vero che per ogni scelta di tali W, T risulta U Å W Å T = V?
- Sia A la matrice:
A =  ,
,
e sia B la seguente base di R3: (e1 + e2, - e3, e2 + 4e3).
- Si dica se l'endomorfismo G di R3 tale che MB(G) =A è diagonalizzabile, e se ne calcolino autovalori e autospazi.
- Sia P una matrice invertibile; è vero che la matrice P -1AP ha gli stessi autovalori e autospazi di A?
| Se vuoi vedere la soluzione  |
 Prova d'esame del 15/10/1996
Prova d'esame del 15/10/1996
Sia G l'endomorfismo di R3 tale che
MB(G) = 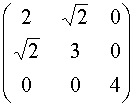 .
.
- Si dica se G è invertibile e se sì, si calcoli la matrice di G -1 rispetto alla base canonica.
- Si calcolino autovalori e autospazi di G e si dica se G è diagonalizzabile.


 Prova d'esame del 8/06/1996
Prova d'esame del 8/06/1996  Prova d'esame del 10/07/1996
Prova d'esame del 10/07/1996 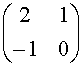 ñ
, W = {
ñ
, W = {
 , a, b Î
R },
T = á
, a, b Î
R },
T = á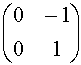 ,
, 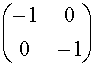 ñ.
ñ. Prova d'esame del 23/09/1996
Prova d'esame del 23/09/1996 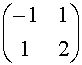 ,
, 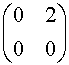 ñ
.
ñ
. ,
,
 Prova d'esame del 15/10/1996
Prova d'esame del 15/10/1996 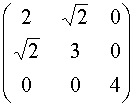 .
.