PA(l ) = det (A - l I) = 0 , cioè
det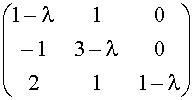 = 0 Û (1 - l
)(l
- 2)2 = 0
= 0 Û (1 - l
)(l
- 2)2 = 0
quindi l = 1 con m1 = 1, l = 2 con m2 = 2.
Determiniamo l'autospazio V1 relativo all'autovalore l = 1, :
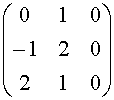
![]() =
= ![]() Û
Û 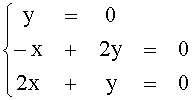 Û
Û 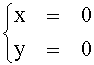
Essendoci una sola variabile libera, dim V1= 1, ed una base si ottiene per esempio ponendo z = 1,
{
(0, 0, 1)}
.Determiniamo l'autospazio V2 relativo all'autovalore l
= 2 :
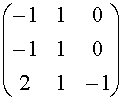
![]() =
= ![]() Û
Û 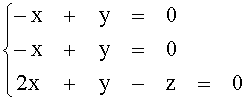 Û
Û
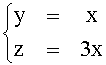
Anche questa volta, essendoci una sola variabile indipendente, dim V2= 1.
Se si pone, per esempio, x = 1 una base dell'autospazio può essere {
(1, 1, 3)}
.
Poiché dim V2= 1 ¹
2 = m2, l'endomorfismo non è diagonalizzabile.
Mostriamo che i polinomi caratteristici coincidono:
PP- 1AP(l ) = det(P - 1AP - l I) = det(P - 1AP - P - 1l IP) = det[P - 1(A - l I)P] =
per il teorema di Binet si ha:
= det(P - 1)det(A - l I)det(P) =
dal momento che i determinanti sono scalari e commutano e che det(P - 1)det(P) = 1 si ha:
= det(A - l I) = PA(l ) .
Mostriamo, con un controesempio relativo alle matrici quadrate, che gli autospazi sono diversi.
Sia A =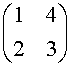 la matrice avente per autovalori l
= 5, l
= -1. Gli autospazi V5, V-1 sono generati rispettivamente dagli autovettori v = (1, 1), w = (2, -1).
la matrice avente per autovalori l
= 5, l
= -1. Gli autospazi V5, V-1 sono generati rispettivamente dagli autovettori v = (1, 1), w = (2, -1).
Sia P = 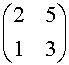 una matrice invertibile, allora
una matrice invertibile, allora
P-1AP = 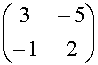
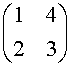
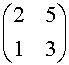 =
= 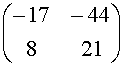 .
.
Determiniamo l'autospazio relativo all'autovalore l = -1,V-1:

![]() =
= ![]() Û x = -
Û x = - ![]() y,
y,
si ha che se, per esempio, si pone y = 4 si ottiene l'autovettore w1 = (-11, 4) ¹ w = (2, -1), quindi gli autospazi sono diversi.