
 (asintoti orizzontali o obliqui) o per x che tende ad un punto ove la f non è definita o è discontinua (asintoti verticali).
(asintoti orizzontali o obliqui) o per x che tende ad un punto ove la f non è definita o è discontinua (asintoti verticali).| ASINTOTI VERTICALI | Si dice che la retta x = c è un asintoto
verticale per
la funzione f se c'è un punto singolare in cui si abbia: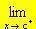 f(x) = ± f(x) = ±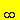 oppure
oppure 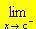 f(x) = ±
f(x) = ±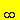 Si dice che l'asintoto è pari se lim f(x)=± 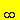 per x che tende a c sia da sx che da dx, e dispari
se i limiti sono discordi.
per x che tende a c sia da sx che da dx, e dispari
se i limiti sono discordi.
|
| ASINTOTI ORIZZONTALI | Si dice che la retta y=l è un asintoto
orizzontale per la funzione f se si verifica una almeno delle seguenti
condizioni: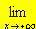 f(x) = l oppure f(x) = l oppure 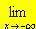 f(x) = l f(x) = l |
| ASINTOTI OBLIQUI | Se si ha 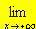 f(x)= ± f(x)= ±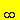 oppure oppure 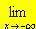 f(x)= ± f(x)= ±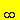 , è lecito chiedersi se esista
un asintoto obliquo, e cioè se il grafico della funzione si accosta (quando x tende a più o meno infinito) a quello di una retta di equazione y=mx+q (ove m ¹ 0, altrimenti si tratterebbe di un asintoto orizzontale); naturalmente possiamo avere due diversi asintoti obliqui per x che tende a più o meno infinito. Quindi in questo caso dobbiamo determinare (se esistono) i valori m e q. , è lecito chiedersi se esista
un asintoto obliquo, e cioè se il grafico della funzione si accosta (quando x tende a più o meno infinito) a quello di una retta di equazione y=mx+q (ove m ¹ 0, altrimenti si tratterebbe di un asintoto orizzontale); naturalmente possiamo avere due diversi asintoti obliqui per x che tende a più o meno infinito. Quindi in questo caso dobbiamo determinare (se esistono) i valori m e q.Per determinare m si calcola il limite: 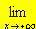  . Se tale limite esiste ed è finito, ci dà il valore di m; si procede allora a calcolare q effettuando il limite . Se tale limite esiste ed è finito, ci dà il valore di m; si procede allora a calcolare q effettuando il limite 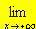 f(x) - mx . f(x) - mx . Di nuovo, se tale limite esiste ed è finito, esso ci dà il valore di q. e quindi l'asintoto obliquo esiste per x che tende a più infinito ed ha equazione y=mx+q . Lo stesso tipo di analisi va compiuto per x che tende a meno infinito. |
| OSSERVAZIONE 1 : | Ci possono essere tanti asintoti verticali, ma al massimo due tra orizzontali e obliqui. Dopo averli trovatoasintoti verticali o obliqui può esser utile calcolare le eventuali intersezioni della curva con essi, risolvendo il sistema composto dall'equazione della curva con quella di ciascun asintoto. |
| OSSERVAZIONE 2 : | Non bisogna cercare nè asintoti orizzontali nè obliqui se il campo di esistenza è un intervallo limitato. |
| OSSERVAZIONE 3 : | Se la funzione è razionale intera non ci sono asintoti di alcun tipo. |
 Esempio
Esempio
 Esercizi
Esercizi


