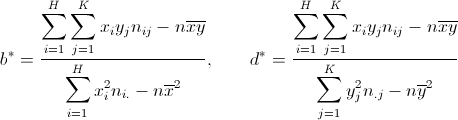9. Metodo di interpolazione dei minimi quadrati |
| |
|
|
| |
Il metodo di interpolazione dei minimi quadrati, che permette di individuare la retta di regressione, consiste nel minimizzare la somma dei quadrati delle differenze tra il valore osservato 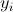 e il valore teorico e il valore teorico 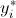 : : |
| |
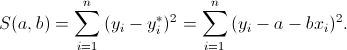 |
(19) |
| |
Ricordando che la distanza euclidea tra due generici punti 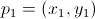 e e 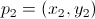 è definita è definita  , la distanza euclidea
tra un valore osservato , la distanza euclidea
tra un valore osservato 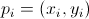 e il corrispondente punto sulla retta e il corrispondente punto sulla retta 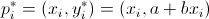 è data da è data da 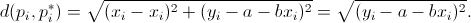 |
| |
Minimizzando la funzione 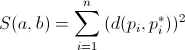 si individueranno i due
parametri si individueranno i due
parametri 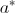 e e 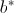 della retta di regressione, la quale minimizza la somma
dei quadrati delle distranze euclidee tra i punti della retta di regressione, la quale minimizza la somma
dei quadrati delle distranze euclidee tra i punti 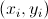 della nuvola dei punti
osservati, data dal grafico di dispersione, e i corrispondenti punti della retta della nuvola dei punti
osservati, data dal grafico di dispersione, e i corrispondenti punti della retta
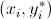 . Più precisamente si dà la seguente . Più precisamente si dà la seguente |
| |
Definizione 41. Si chiama retta di regressione la retta di equazione
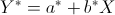 , dove la coppia , dove la coppia 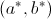 minimizza in minimizza in 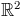 la funzione di due
variabili la funzione di due
variabili 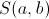 definita da (19). definita da (19). |
| |
Il problema della determinazione della retta di regressione è risolto dalla
seguente |
|
| |
Proposizione 42. I valori che minimizzano 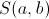 sono dati da sono dati da |
|
| |
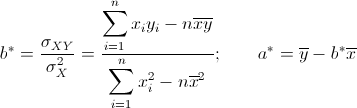 |
(20) |
| |
dove 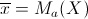 , , 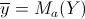 e e 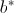 è detto coefficiente di regressione. è detto coefficiente di regressione.
La retta di regressione che meglio si adatta ai dati osservati è dunque data
da 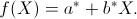 Sostituendo le espressioni trovate si ottiene Sostituendo le espressioni trovate si ottiene |
| |
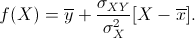 |
(21) |
| |
Dimostrazione.  |
|
| |
Osservazione 6. 1. Il coefficiente di regressione, così come 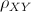 , è un indice
che misura la dipendenza lineare tra due caratteri, con la differenza che , è un indice
che misura la dipendenza lineare tra due caratteri, con la differenza che 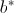 è un indice asimmetrico, cioè assume un valore diverso se si scambia
il ruolo assunto dai due caratteri. è un indice asimmetrico, cioè assume un valore diverso se si scambia
il ruolo assunto dai due caratteri.
2. Il coefficiente di regressione 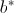 varia in varia in 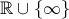 e ha come unità di
misura il rapporto tra le unità di misura di Y e X. Esso indica, a meno
di e ha come unità di
misura il rapporto tra le unità di misura di Y e X. Esso indica, a meno
di  , di quanto varia Y in corrispondenza di una variazione unitaria di
X. , di quanto varia Y in corrispondenza di una variazione unitaria di
X.
3. 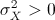 sempre, quindi il segno di sempre, quindi il segno di 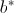 è determinato dal segno di è determinato dal segno di 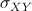 . .
4. Se X e Y sono statisticamente indipendenti allora 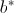 =0; tuttavia non
vale il contrario poiché, come si è visto, =0; tuttavia non
vale il contrario poiché, come si è visto, 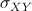 può annullarsi anche
quando non vale l'indipendenza tra i caratteri. Nel caso può annullarsi anche
quando non vale l'indipendenza tra i caratteri. Nel caso 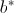 =0 la
retta di regressione è parallela all'asse delle ascisse e interseca l'asse
delle ordinate nel punto =0 la
retta di regressione è parallela all'asse delle ascisse e interseca l'asse
delle ordinate nel punto 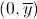 . .
5. Tutti i punti del piano che soddisfano il sistema normale appartengono
alla retta di regressione, quindi anche il baricentro 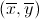 appartiene a
tale retta, come si può facilmente verificare. appartiene a
tale retta, come si può facilmente verificare. |
| |
In maniera analoga a quanto svolto finora, avendo esaminato la relazione
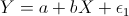 , si può esaminare la relazione , si può esaminare la relazione 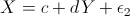 , per la quale
si ottengono risultati analoghi. In particolare, i parametri che si possono
ottenere con il metodo dei minimi quadrati sono , per la quale
si ottengono risultati analoghi. In particolare, i parametri che si possono
ottenere con il metodo dei minimi quadrati sono |
| |
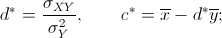 |
(23) |
| |
quindi la retta di regressione che rappresenta X in funzione di Y diventa |
|
| |
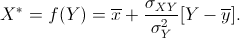 |
(24) |
| |
Osservazione 7. Se si considera la tabella a doppia entrata di due caratteri
X e Y suddivisi rispettivamente in H e K classi, le formule (20) e (23)
per i coefficienti di regressione diventano |
| |
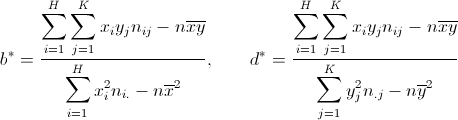 |
(25) |
| |
in cui 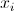 e e 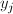 sono rispettivamente i valori centrali dell'i-esima classe di X e
della j-esima classe di Y. sono rispettivamente i valori centrali dell'i-esima classe di X e
della j-esima classe di Y. |
| |
|
 |
|
 |
|
 |
 |
|
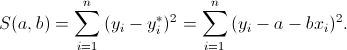
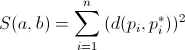 si individueranno i due
parametri
si individueranno i due
parametri 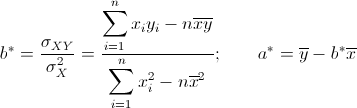
![]() , è un indice
che misura la dipendenza lineare tra due caratteri, con la differenza che
, è un indice
che misura la dipendenza lineare tra due caratteri, con la differenza che ![]() è un indice asimmetrico, cioè assume un valore diverso se si scambia
il ruolo assunto dai due caratteri.
è un indice asimmetrico, cioè assume un valore diverso se si scambia
il ruolo assunto dai due caratteri.![]() varia in
varia in ![]() e ha come unità di
misura il rapporto tra le unità di misura di Y e X. Esso indica, a meno
di
e ha come unità di
misura il rapporto tra le unità di misura di Y e X. Esso indica, a meno
di ![]() , di quanto varia Y in corrispondenza di una variazione unitaria di
X.
, di quanto varia Y in corrispondenza di una variazione unitaria di
X.![]() sempre, quindi il segno di
sempre, quindi il segno di ![]() è determinato dal segno di
è determinato dal segno di ![]() .
.![]() =0; tuttavia non
vale il contrario poiché, come si è visto,
=0; tuttavia non
vale il contrario poiché, come si è visto, ![]() può annullarsi anche
quando non vale l'indipendenza tra i caratteri. Nel caso
può annullarsi anche
quando non vale l'indipendenza tra i caratteri. Nel caso ![]() =0 la
retta di regressione è parallela all'asse delle ascisse e interseca l'asse
delle ordinate nel punto
=0 la
retta di regressione è parallela all'asse delle ascisse e interseca l'asse
delle ordinate nel punto ![]() .
.![]() appartiene a
tale retta, come si può facilmente verificare.
appartiene a
tale retta, come si può facilmente verificare.