Per determinare il minimo della funzione , si deve innanzitutto imporre la condizione per la ricerca dei punti critici.
Dalla condizione si ottiene un sistema di due equazioni in due incognite, detto sistema normale:

Ricordiamo la Definizione 13 di media aritmetica nella formulazione (1) e utilizziamo le notazioni e . Il sistema normale (22) può essere così risolto

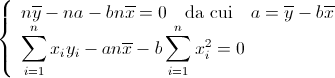
Nella seconda equazione sostituiamo e ricordiamo la Definizione 16 di varianza e 35 di covarianza, in particolare nelle loro scritture equivalenti (9) e (12). Si avrà: , da cui si può ricavare b. In definitiva si ottiene

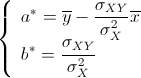
Per verificare che la coppia rappresenta un minimo per introduciamo la matrice Hessiana definita da

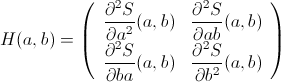
che deve risultare definita positiva in . Ricordiamo che se è una matrice reale nxn simmetrica, essa è definita positiva se e solo se e . Per la matrice si ha

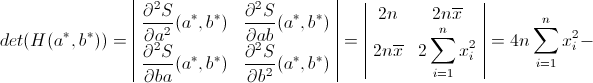
Poiché , la Proposizione 42 risulta dimostrata.

CVD