|
Siano A,B e C eventi. Trova le espressioni
algebriche in termine di intersezioni, unioni e complementazione, per gli eventi
costituiti dal fatto che tra A,B e C si verificano:
1) soltanto A;
2) sia A sia B ma non C;
3) almeno uno dei tre;
4) almeno due dei tre;
5) tutti i tre;
6) nessuno dei tre;
7) non più di un evento;
8) non più di due eventi;
9) esattamente due eventi;
Soluzione
|
Calcolare
la probabilità che esca una figura in un mazzo di 52 carte da gioco.
Soluzione
|
|
Calcolare la probabilità che esca una sola testa lanciando due volte una
moneta.
Soluzione
|
|
Calcolare la probabilità che lanciando 3 monete:
A – escano
due teste
B – non esca
nessuna testa
C – esca una
sola testa
D – escano
tre teste
Soluzione
|
|
Calcolare la probabilità che lanciando due dadi:
A) - la somma sia 5 e
B) - escano due 1
Soluzione
|
In un’urna
ci sono 3 palline bianche e 2 nere. Calcolare la probabilità che in due
estrazioni
(reintroducendo
la pallina estratta, prima di estrarre la seconda pallina ):
A - escano
due palline nere *
B - escano
due palline bianche +
C - due
palline di diverso colore -
Soluzione
|
|
Calcolare
la probabilità di estrarre tre assi di seguito da un mazzo di 52 carte ( carte
francesi ).
Soluzione
|
Trovare la probabilità di
estrarre il re di cuori oppure l'asso di picche da un mazzo di 52 carte.
Soluzione
|
Abbiamo
un sacchetto con 10 palline bianche, 20 rosse e 30 nere: trovare la probabilità
di estrarre una pallina bianca oppure nera.
Soluzione
|
Nel
gioco della roulette vi sono 36 numeri più lo zero.
Trovare la probabilità dell'uscita alla roulette di
un numero compreso tra 5 e 9 (compresi) oppure multiplo di 10.
Soluzione
|
Trovare la probabilità che
su una determinata ruota del lotto esca il numero 2.
Soluzione
|
|
Il
Cavaliere di Méré pose al matematico Pascal il seguente quesito sul gioco dei
dadi: "L'uscita di un 6 lanciando quattro dadi dovrebbe avere la stessa
probabilità di avere almeno una coppia di 6 lanciando per 24 volte una coppia
di dadi. Come mai il primo evento sembra verificarsi invece con maggiore
frequenza del secondo?"
Soluzione
|
Elena compie gli anni in giugno. Di seguito è riportato il
calendario di giugno 2010, dove sono evidenziati i giorni festivi.
Qual è la probabilità che Elena compia gli anni in un giorno
festivo?

Soluzione
|
Tre scatole A, B e C contengono lampade prodotte da una certa fabbrica di cui alcune difettose.
A contiene 2000 lampade con il 5% di esse difettose, B ne contiene 500 con il 20% difettose e
C ne contiene 1000 con il 10% difettose. Si sceglie una scatola a caso e si estrae a caso una lampada.
Quale è la probabilità che essa sia difettosa?
Soluzione
|
|
Un’urna
contiene 10 palline di cui 6 rosse e 4 bianche. Si estraggono, successivamente
l’una all’altra, 2 palline.Calcolare la probabilità che entrambe le palline
sono rosse nell’ipotesi che ci sia o non ci sia reimmissione.
Soluzione
|
Un’urna
contiene 6 gettoni neri, 5 rossi e 4 bianchi.
Estraendo a caso un gettone si
può verificare uno dei seguenti eventi:
E1 = « estrazione di un
gettone nero »
E2 = « estrazione di un
gettone rosso »
E3 = « estrazione di un
gettone bianco »
E4
= « estrazione di un gettone nero o rosso »
E5 = « estrazione di un
gettone rosso o bianco »
E6 = « estrazione di un
gettone nero o rosso o bianco »
Soluzione
|
Consideriamo un bersaglio circolare.
Qual è la
probabilità di colpire a caso un punto più vicino al centro che alla circonferenza?
Soluzione
|
|
Qual è la probabilità che un
punto scelta a caso nel quadrato, sia interno alla circonferenza inscritta ?
Soluzione
|
Consideriamo un segmento AB e prendiamo un punto a caso su di
esso.
Qual è la probabilità che questo punto sia il punto medio del
segmento?
Soluzione
|
|
Una moneta da 2 euro (il suo
diametro è 25,75 mm) viene lanciata su un pavimento ricoperto con
mattonelle quadrate di lato 10 cm. Quale è la probabilità che la moneta vada a
finire internamente ad una mattonella?
(cioè non tagli i lati dei quadrati)
Soluzione
|
Il problema della moneta di Buffon
Qual è la probabilità che una moneta che cade su un pavimento piastrellato intercetti il bordo della piastrella?
Soluzione - caso piastrelle quadrate con lato unitario
Soluzione - caso piastrelle rettangolare con i lati 2a e 2b |
Un
meteorite cade sulla Terra; qual è la probabilità che il punto d’incontro si
trovi fra l’equatore e il tropico del Cancro (latitudine λ = 23° 27’ nord)?
Soluzione |

Soluzione |
|
Antonio e Bruno decidono che il conto del Bar sarà
pagato da colui che pesca la carta più bassa. Per evitare la parità, decidono
di usare solo le 13 carte di uno stesso seme. Antonio pesca un 5. Che
probabilità ha ora Bruno di non pagare il conto?
Soluzione |
|
Si hanno 7 lampadine buone ( B ) e 3 rotte ( R ).
Calcolare la probabilità che estraendone due a caso (senza reinserire la prima
lampada) siano entrambe buone.
Soluzione |
|
Anna e
Francesca hanno rispettivamente probabilità 1/2 e 1/5 di superare l'esame, e la probabilità che
entrambe superino l'esame è 1/10. Determinare la probabilità che
almeno una delle 2 superi l'esame.
Soluzione
|
|
In un’urna ci sono tre palline nere e due bianche. Calcolare la probabilità che esca prima una nera e
dopo una bianca senza reimmissione nell’urna della prima pallina.
Soluzione |
|
In un paese scandinavo il 70% delle ragazze ha i
capelli Biondi, il 20% li ha Rossi, il 10% Mori. Risulta poi che ha gli occhi
Scuri 10% delle Bionde, il 25% delle Rosse,il 50% delle More. Se la ragazza con
cui ho fatto amicizia tramite Internet mi fa sapere che ha occhi Scuri, che
probabilità c'è che sia Bionda?
Soluzione
|
Una
compagnia di assicurazioni auto prevede per i guidatori giovani una polizza più
alta, in quanto questo
gruppo tende ad avere un numero maggiore di incidenti. La compagnia distingue
le età in 3 gruppi:
A
(sotto i 25 anni, 22% di tutti i suoi assicurati),
B (25-39 anni, 43%),
C (da
40 anni in su).
I dati
mostrano che in media ogni anno le percentuali di assicurati che hanno un
incidente sono:
11% per
il gruppo A, 3% per il B, 2% per il C.
a) Che percentuale di assicurati ci si attende abbia un
incidente nei prossimi 12 mesi?
b) Se
un assicurato X ha appena avuto un incidente, che probabilità c’è che abbia
meno di 25 anni?
Soluzione
|
|
In un bar ci
sono due macchinette mangiasoldi A e B. Effettuando una singola giocata su A si
vince con la probabilità 1/2 ( in altre parole: si vince mediamente 1 volta su 2,
o, se preferisci, all'incirca 500 volte su 1000) mentre giocando su B si vince
con la probabilità 1/4.
Supponiamo
di non sapere quale sia la macchinetta A e quale la B;
se ne
scegliamo una a caso, giochiamo una sola volta, e vinciamo, che probabilità c'è
che la macchinetta scelta sia stata A ?
Soluzione
|
|
In una certa facoltà universitaria, è obbligatorio sostenere un esame di Lingua Straniera.
Ogni studente può scegliere
fra:
Inglese, Francese, Spagnolo, Tedesco.
Le statistiche dicono che le probabilità di scelta sono rispettivamente:
0,4 0,3 0,2 0,1
D'altra parte, per la diversa difficoltà dei corsi e severità degli
insegnanti, le
probabilità di riportare la massima votazione (30 trentesimi) variano da
lingua
a lingua e sono rispettivamente:
0,1 0,2 0,3 0,9
Supponiamo di sapere che un certo studente ha riportato 30 trentesimi
nell'esame di Lingua.
Che probabilità c'è che la materia d'esame sia stata Inglese?
Soluzione
|
|
Un'urna contiene 2 biglie bianche e 5 nere. Estraiamo una prima biglia;
se è nera la rimettiamo dentro con altre due dello stesso colore, se è
bianca non rimettiamo niente. Estraendo la seconda biglia, qual è
la probabilità che sia nera?
Soluzione |
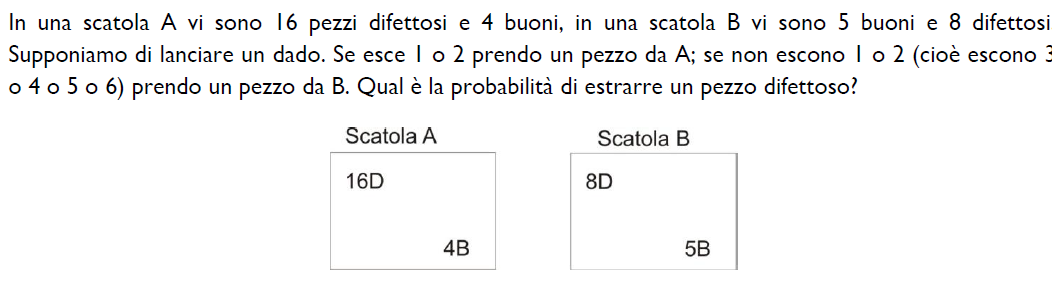
Soluzione |
Determinare la probabilità che un numero di 4 cifre in base 10, abbia almeno 2 cifre uguali.
Soluzione |

Soluzione |
Un
certo tipo di missile ha la probabilità 0,30 di colpire il
bersaglio. Quanti missili si devono lanciare affinché la
probabilità di colpire il bersaglio almeno una volta, sia almeno
80 % ?
Soluzione |

Determinare la probabilità che un certo individuo abbia la tubercolosi, dato che risulta positivo al test.
Soluzione |
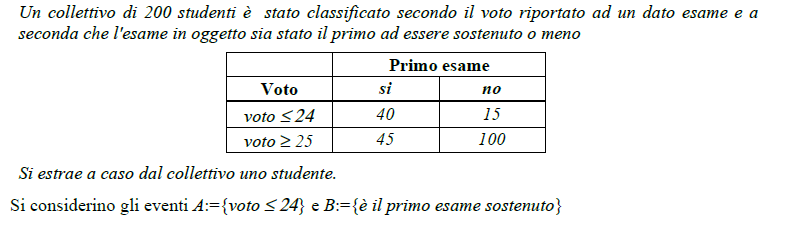
Calcolare P(A), P(B), P(AUB), P(A | B)
Soluzione |

Soluzione |
Si lanciano
due dadi.
1. Qual è la probabilità che almeno uno di essi sia
un 6?
2. Trova la probabilità che il 6 non compaia su
nessuno dei due dadi.
3. Trova
la probabilità che le due facce presentino numeri diversi tra loro.
|
Da una partita di 1000 confezioni di pasta ne estraggo due per controllare se il peso è al di sotto di quello dichiarato.
Sapendo
che la partita contiene 10 confezioni difettose qual è la
probabilità che entrambe le confezioni estratte siano sottopeso?
Soluzione |
Supponiamo
che i pezzi prodotti da una certa macchina possono presentare due tipi
di difetti, che chiameremo a e b. E' stabilito che la
probabilità che un pezzo presenti il difetto a è 0,1, la
probabilita che non presenti il difetto b è 0,8, la
probabilità che presenti entrambi i difetti è 0,01.
Qual'è la probabilità che un pezzo non presenti alcun difetto?
|
|
Problema delle tre carte: supponiamo di avere
tre carte da gioco, una con faccia rossa e l'altra nera, una con entrambe le
facce rosse e una con entrambe le facce nere. Si estrae una carta a caso e la
si mette sul tavolo. Se la faccia visibile è rossa, qual è la probabilità che
la faccia coperta sia rossa?
Soluzione |
 Torna all'Indice
Torna all'Indice  Torna all'Indice
Torna all'Indice