|
- "Affermo
che nessuna scienza mi sembra più utile, più bella e più facile della
matematica. Ed invero: quale altra scienza si occupa di verità più
elementari, poiché essa non ne presuppone alcun’altra, mentre ogni
altra presuppone la matematica? In quale altra scienza le
argomentazioni sono altrettanto convincenti ed esaurienti? Quale altra
scienza conduce a risultati più sicuri e più agevolmente controllabili?
In quale altra scienza meglio rifulge lo splendore del vero? Quale
altra fornisce cognizioni tanto universali nel tempo e nello spazio? La
matematica è universalmente utile, oltre e forse più che per la verità
che essa fa conoscere, per i metodi di ricerca che essa adopera ed
adoperando insegna. Nessun altro studio richiede meditazione più
pacata: nessun altro meglio induce ad esser cauti nell’affermare,
semplici ed ordinati nell’argomentare, precisi e chiari nel dire "
Alessandro Padoa (1868-1937) , 1908 - "Elogio alla matematica".
-
La stima della probabilità di un evento
è uno strumento fondamentale della statistica. Nelle sue forme
più semplici, si fonda sul calcolo combinatorio. E’
evidente ed intuitiva la sua applicazione ai giochi d'azzardo, ai quali
effettivamente fu associata alla sua origine. Anche se il risultato di
ogni singolo tentativo è imprevedibile, con un numero elevato di
ripetizioni si stabiliscono regolarità che possono essere
previste e calcolate. Dal punto di vista didattico,
l’associazione del concetto di probabilità al calcolo
combinatorio è un aspetto importante: serve per collegare una
scelta alla probabilità con la quale l'evento atteso può
avvenire, nel contesto di tutti gli eventi alternativi possibili.
E’ la base dell’inferenza statistica, della scelta
scientifica in tutti i casi d’incertezza.
I concetti e i metodi del calcolo combinatorio possono essere spiegati in modo semplice, attraverso il seguente esempio.
Esempio 1:
In una corsa con 10
concorrenti, che abbiano le medesime possibilità di vittoria,
è possibile porsi molti quesiti, tra i quali:
a) quanti differenti ordini d'arrivo sono possibili?
b) quale è la probabilità di indovinare i primi 3 al traguardo, secondo l'ordine?
c) quale la probabilità di indovinare i primi 3, senza considerare il loro ordine?
d) è conveniente scommettere 10 euro per guadagnarne 500 euro, se si indovinassero i primi 2 nell'ordine?
e) è conveniente senza stabilire l'ordine?
Per calcolare le
probabilità richieste, occorre prestare attenzione alle 4
caratteristiche fondamentali di questi eventi:
(1) si escludono a vicenda,
(2) sono tutti ugualmente possibili,
(3) sono casuali,
(4) sono indipendenti.
a) In una corsa con 10 concorrenti, i possibili ordini d'arrivo sono le permutazioni di 10 elementi.
Il loro numero è: P = 10! = 1⋅2⋅3⋅4⋅5⋅6⋅7⋅8⋅9⋅10 = 3. 628.800
-
b)
In una corsa di 10 concorrenti, il numero dei possibili gruppi
differenti formati dai primi 3 all’arrivo, tenendo conto anche
del loro ordine, sono le disposizioni di 10 elementi 3 a 3, cioè
:
-
La probabilità di indovinare i primi 3 concorrenti secondo l'ordine d'arrivo è: 1 / 720 = 0,001389.
c)
In una corsa di 10 concorrenti, i possibili gruppi dei primi 3
concorrenti, senza distinzioni interne di ordine, sono le combinazioni
di 10 elementi 3 a 3, cioè:
La
probabilità di indovinare i primi 3 concorrenti, senza
stabilirne l'ordine, è 1/120 = 0,008333; è 6 ( = 3!)
volte più alta di quella in cui si chiede di indovinare anche il
loro ordine.
d)
Il numero di possibili gruppi formati dai primi 2 concorrenti,
stabilendo chi sarà il primo e chi il secondo, in un gruppo di
10 è determinato dalle disposizioni di 10 elementi 2 a 2,
cioè :
La
probabilità di indovinare chi saranno i primi 2 è uguale
a 1/90. E un rapporto più sfavorevole del rapporto di 1 a 50
fissato nella scommessa (10 euro contro 500 euro). Per chi scommette
non è conveniente vincere 50 volte la posta, quando la
probabilità di vincere è 1/90.
e)
Il numero di possibili gruppi formati dai primi 2 concorrenti, senza
stabilire l'ordine, in un gruppo di 10 è dato dalle combinazioni
di 10 elementi 2 a 2, cioè :
La
probabilità di indovinare i primi 2 senza dover stabilire
l’ordine uguale a 1/45; è più favorevole del
rapporto di 1 a 50 fissato dalla scommessa. Per chi scommette è
conveniente, perché l’eventuale guadagno è
superiore al rischio. Una scommessa tra i due giocatori è in
parità, solamente quando il prodotto tra la probabilità
d’indovinare e il moltiplicatore della posta è uguale a 1.
Esempio 2:
Ho quattro scatole chiuse,
numerate da 1 a 4, e so che dentro ci sono complessivamente tre palline
(ma non so come queste siano distribuite nelle scatole).
Che probabilità ho che le tre palline siano tutte nella scatola n. 1?
Gli eventi elementari, che possono essere considerati equiprobabili,
sono le possibili distribuzioni delle tre palline nelle quattro
scatole. Detto ciò, risolviamo l’esercizio in due modi
diversi:
1 metodo (“diretto”).
Contiamo i casi possibili e i casi favorevoli. I casi fa-vorevoli sono
solamente uno (la configurazione in cui le tre palline sono nella
scatola 1). Contare i casi possibili è facile: ci sono 4
configurazioni in cui le tre palline sono tutte in una sola scatola e 4
in cui le tre palline sono tutte in scatole diverse. Restano i casi di
tipo 2+1 (due palline nella stessa scatola, una in una scatola diversa
e due scatole vuote): le due scatole vuote possono essere scelte in 6
modi diversi e per ogni scelta delle due scatole vuote restano 2
possibilità per mettere la pallina singola. Dunque le
configurazioni di tipo 2+1 sono 6 × 2 = 12. Complessivamente
abbiamo contato 4 + 4 + 12 = 20 casi possibili e pertanto la
probabilità cercata è: 1/20.
2 metodo (applicazione delle formule del calcolo combinatorio).
Osserviamo che posso interpretare il“mettere una pallina in una
scatola” come lo “scegliere” quella scatola e il
“mettere due palline” in una scatola come lo
“scegliere due volte” quella scatola, "mettere tre palline"
in una scatola come lo "scegliere tre volte" quella scatola. Allora una
distribuzione delle tre palline nelle quattro scatole la posso vedere
come una scelta, con possibili ripetizioni, di tre scatole dalle
quattro disponibili. In altre parole, `e una combinazione con
ripetizioni di 4 oggetti presi tre alla volta (nel linguaggio
paste-vassoio: è come se dovessi riempire un vassoio con tre
paste scegliendole da quattro tipi diversi). Dunque i casi possibili
sono 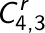 mentre
il caso favorevole è, come già detto, uno solo: tutte e
tre le palline nella prima scatola, ovvero la prima scatola
“scelta tre volte”. La probabilità è : mentre
il caso favorevole è, come già detto, uno solo: tutte e
tre le palline nella prima scatola, ovvero la prima scatola
“scelta tre volte”. La probabilità è :
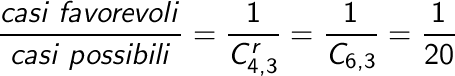
Da evidenziare il fatto che questo secondo metodo è migliore quando si ha a che fare con numeri grandi.
Esempio 3:
Esame di stato, tema di matematica n 1 (PNI, a. s. 2000-2001- Corso di
ordinamento. Liceo scientifico). Il quesito n° 8 è
l’unico di probabilità. Si chiede:
Una classe è
composta da 12 ragazzi e 4 ragazze. Tra i sedici allievi se ne
scelgono tre a caso: qual è la probabilità che essi siano
tutti maschi?
1 metodo:
uso del calcolo combinatorio. Si valuta che il numero di casi
favorevoli è il numero di combinazioni di classe 3 di 12
elementi:
mentre il numero di casi possibili
è quello delle combinazioni di classe 3 di 16 elementi:
La probabilità dell’evento che si considera è allora data dalla classica formula:
2 metodo: uso della probabilità condizionata.
Si immagina di osservare, uno dopo l’altro, i tre allievi
sorteggiati e per i∈{1, 2, 3} si considera l’evento Mi =
“Lo studente dell’i-sima osservazione è
maschio”. Allora l’evento di cui si chiede la
probabilità è il prodotto logico M1M2M3 e, per il teorema
della probabilità composta:
P(M1M2M3) = P(M1) P(M2/M1) P(M3/M1M2) = 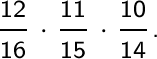
|
|
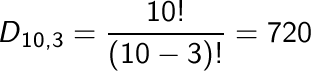
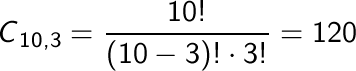
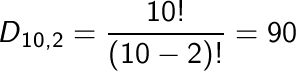
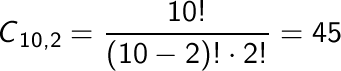
 mentre
il caso favorevole è, come già detto, uno solo: tutte e
tre le palline nella prima scatola, ovvero la prima scatola
“scelta tre volte”. La probabilità è :
mentre
il caso favorevole è, come già detto, uno solo: tutte e
tre le palline nella prima scatola, ovvero la prima scatola
“scelta tre volte”. La probabilità è : 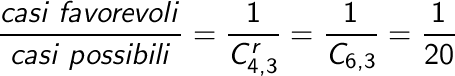
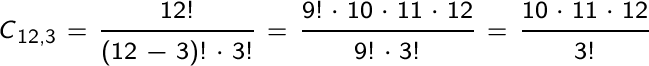
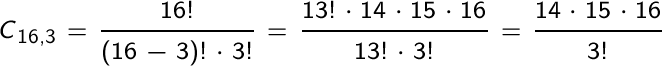
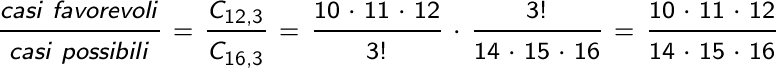
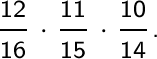

 Torna all'Indice
Torna all'Indice  pagina successiva
pagina successiva