Supponiamo per assurdo che:

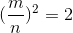
riduciamo poi la frazione ai minimi termini ed otterremo che:


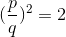
con MCD(p,q)=1; ne verrà quindi che
p²=2q²
e quindi che p² è pari e anche p è pari, cioè
∃ p'∈ ℤ t.c. p=2p'.

Ma allora
(2p')²=2q² cioè q²=2p'²
cioè q² è pari e anche q è pari, ma questo è un assurdo poichè avevamo assunto MCD(p,q)=1, cosicchè questo conclude la prova del teorema. □