15 OSSERVAZIONE
I sottospazi affini non banali (diversi cioè dai punti e da
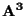
stesso) di
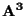
sono i piani e le rette.
Sia
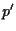
un piano di
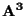
di equazione
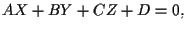
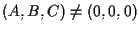
Allora la chiusura proiettiva
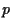
di
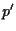
in
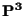
è il piano di
equazione
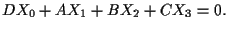
I punti impropri di
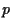
rispetto a
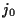
sono i punti della retta
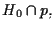
ovvero i punti
![$[0,l,m,n]$](img10.gif)
tali che
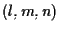
è soluzione non banale
dell'equazione
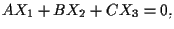
cioè tali che
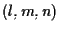
è un vettore non
nullo di
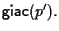
Quindi l'insieme dei punti impropri rispetto a
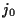
di
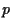
coincide con la retta
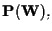
dove
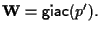
Consideriamo ora una retta
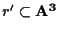
di equazioni cartesiane
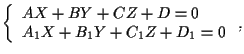 con
con
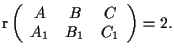
La chiusura proiettiva di 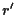 è la retta
è la retta
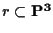 di
equazioni cartesiane
di
equazioni cartesiane
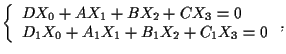 dove
dove
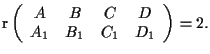
La retta 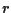 consiste dei punti propri di
consiste dei punti propri di 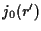 e del punto improprio
e del punto improprio
![$[0,l,m,n],$](img25.gif) dove
dove 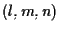 è un vettore di direzione di
è un vettore di direzione di 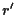 e soddisfa il
sistema
e soddisfa il
sistema
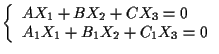
 che descrive precisamente
che descrive precisamente
16 OSSERVAZIONE
Sia
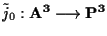
un completamento
proiettivo dello spazio affine
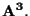
Allora ogni retta
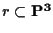
non contenuta in
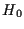
è la
chiusura proiettiva di una retta
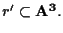
I piani contenenti
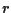
sono tutte e sole le chiusure proiettive dei piani di
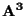
del
fascio di asse
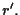
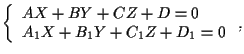 con
con
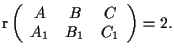
![]() è la retta
è la retta
![]() di
equazioni cartesiane
di
equazioni cartesiane
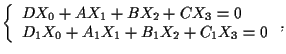 dove
dove
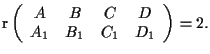
![]() consiste dei punti propri di
consiste dei punti propri di ![]() e del punto improprio
e del punto improprio
![]() dove
dove ![]() è un vettore di direzione di
è un vettore di direzione di ![]() e soddisfa il
sistema
e soddisfa il
sistema
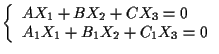
![]() che descrive precisamente
che descrive precisamente
![]()




